DEMANDES

SALAM
jé présenté une démo au prof mais ila refusé je sais pas pourkoi
pour montrer que si a²|b²==>a|b
le (<== et évident
jé fé comm sa :
on va travaiallé dabord ke pour les a,b>0
(a²/b²=n ==> a/b=Vn)
or si Vn £ Q <==>n=m²
jé comm sa
Vm=p/q (PGCD)(p;q)=1
==> m=p²/q² ==> p²=m et q²=1 (parcke p² et q² sont premier entre eux)
donc pour que le Vn=a/b ifo que Vn=p £ IN
CQFD
2eme demande
pour ceux kissont interessé par l'informatique
jé fé un algorithme (sur PASCAL) qui te dit si le nombre est premier ou pas
or je ne peu po déclare que "longint" alors je px entrer que 9 caracteres
je veu savoir eske je peu faire une déclaration qui me donnera plus de caracteres (jé cherché mai jé rien trouvé :S)
A+

J'ai pas très bien saisie ton raisonnement mais bon voici ce que je propose .
On fait le décomposition de a,b,m avec a²=mb²
On pose :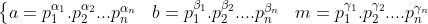

Avec certain alpha,beta,gamma=0 pour les nombre premier qui ne sont pas des diviseurs commun de a,b et m .
Donc on a :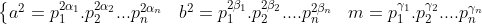

et :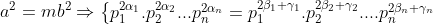

Et puisque b²/a² alors on aura :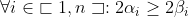
et donc : 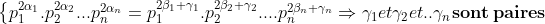et psk gamma_{i} est positif Donc m est un carré parfait .
CQFD

c vraiment ce que jé fé !!

houssam110 a écrit:

2eme demande
pour ceux kissont interessé par l'informatique
jé fé un algorithme (sur PASCAL) qui te dit si le nombre est premier ou pas
or je ne peu po déclare que "longint" alors je px entrer que 9 caracteres
je veu savoir eske je peu faire une déclaration qui me donnera plus de caracteres (jé cherché mai jé rien trouvé :S)
A+

Avec "long int", la taille limite du nombre que tu peux entrer est fixée à 9 chiffres, et tu souhaites franchir cette contrainte ? Telle est donc ta question ?
Mais un nombre à 9 chiffres, c'est pas amplement suffisant, alors ?

oui jlé déja cité "longint" me permet juste d'entre 9 caraactere
or moi je vx lapliker pour n'importe kel nombre de IN
je sé po si je px travailler sous des intervalles?
mais sa seré difficil
car je vx faire un algoroithme qui peu déterminer n'importe kel nombre premier!!

houssam110 a écrit:

oui jlé déja cité "longint" me permet juste d'entre 9 caraactere
or moi je vx lapliker pour n'importe kel nombre de IN
[...]
car je vx faire un algoroithme qui peu déterminer n'importe kel nombre premier!!

Il est préférable d'innover sur des questions au goût du jour, plutôt que de rabâcher sur des questions maintes fois débattues, et devenues stériles à l'excès. Les algorithmes ayant pour tâche le test de primalité sont nombreux, de type et de masse, et n'attendent sûrement pas qu'un néophyte attardé lève le bout du nez pour les soigner.

houssam110 a écrit:

je sé po si je px travailler sous des intervalles?
mais sa seré difficil

Tu baisses donc déjà les bras ? Eh, ton parcours en programmation promet d'être bien prodigieux !

je vs rien soigner moi je voulé juste savoir eske je peu faire une déclaration de variables ki me permet d'entrer plus de caractere
un peu d'humilité sa va rien couter ...

houssam110 a écrit:

je vs rien soigner moi je voulé juste savoir eske je peu faire une déclaration de variables ki me permet d'entrer plus de caractere
un peu d'humilité sa va rien couter ...

Je ne manipule pas souvent le pascal. Cela dit, la documentation semble indiquer qu'il existe un type "Int64", qui fait 8 bytes, et qui peut par conséquent contenir bien plus qu'un "Longint", qui lui, fait seulement 4 bytes.