- galillee56 a écrit:
- exo arithemetique: soit a et b dans N tq pour tout n dans N a^n-1 divise b^n-1 montrer qu'il existe d dans N tq b=a^d
Je propose ma solution:
Je pense qu'il faut éliminer le cas où
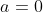
car il ne permet pas de conclure.
Premièrement, on s'en sert des deux hypothèses
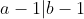
et
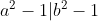
pour démontrer que
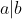
.
Soit
)
, alors ils existent deux entiers
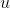
et

tels que:
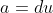
,
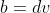
et
=1)
.
Puisqu'on a
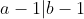
, alors
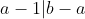
et il va exister un entier

tel que
)
.
Ce qui donne
)
, soit
=k)
et donc
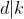
.
Cela se traduit par l'existence d'un entier

tel que
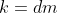
.
Alors
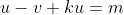
, soit
-v=m)
.
Donc
=m)
, et du coup
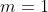
.
Alors
)
.==>(1)
De même, on aboutit à
)
.
Cette dernière égalité s'écrit:
d(a-1)=d^2(a-1)(a+1))
.
Si
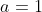
, et sachant que

ne peut diviser que lui même il s'ensuit que
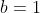
.
Sinon, on aura
)
.==>(2)
En sommant (1) et (2), on aura que
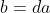
.
On aura alors:
: a^n-1|d^n-1)
et par suite
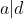
.
Il existe alors
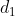
tel que
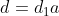
.
On a ainsi:
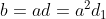
.
Et on continue ainsi: à l'étape
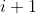
, on écrit:
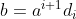
et on a
:a^n-1|d_i^n-1)
.
(On a:
:a^n-1|b^n-1-(a^n-1)=b^n-a^n=a^n(a^{in}.d_i^n-1))
, donc
:a^n-1|a^{in}.d_i^{n}-1)
car
:a^n-1\text{ ne divise pas }a^n)
.
Donc
:a^n-1|a^{in}.d_i^n-1-(a^n-1)=a^n(a^{(i-1)n}.d_i^n-1))
, soit pour la même raison
:a^n-1|a^{(i-1)n}d_i^n-1)
.
Et on continue ainsi jusqu'à:
:a^n-1|d_i^n-1)
.)
Pour

fixé, la suite
_{i\in\mathbb{N}})
est décroissante minorée, donc convergente.
S'agissant d'une suite d'entiers, elle est stationnaire à partir d'un certain entier

.
Par conséquent, la suite tend vers
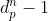
qui va être inférieur à
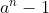
.
On a donc deux cas:
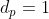
ou
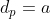
.
Dans tous les cas, c'est gagné et on a
: b=a^d)
.
CQFD.
Sauf erreurs.
