- ayoubmath a écrit:
- salam
1-- soit E un espace vecto normé de dim finie
montrer que pour tout ouvert de E on peut y extraire une base
La question me semble mal posée.
Ce que j'ai compris est qu'il faut montrer qu'on peut extraire une base de tout ouvert

(non vide) inclus dans

de dimension finie

. Et voici ma proposition de résolution:
Soit

un ouvert non vide de

, et soit
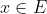
.
Alors, il existe une boule
\subset A)
où
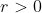
est son rayon.
Soit
)
la base canonique de

.
On pose:
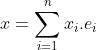
.
Puisque toutes les normes sont équivaletes en dimension finie, on travaille avec la norme infinie

définie par:
:N(y)=\max_{1\le i\le n}{|x_i|})
.
On a
:\sum_{i=1}^{n}x_i\neq\frac{r}{2p})
.
On pose:
: y_i=x-\frac{r}{2p}.e_i)
.
On a
: N(x-y_i)<r)
, donc
: y_i\in B(x,r)\subset A)
.
Montrons que
)
est une base de

.
Il suffit de montrer que cette famille est libre, car son cardinal est

.
Supposons que:
:\sum_{i=1}^{n}\alpha_i.y_i=0)
.
On a:
=0)
. D'où:
: x_j\sum_{i=1}^{n}\alpha_i-\frac{r}{2p}\alpha_j=0)
(cela découle de la projection sur
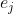
).
En sommant, on aura:
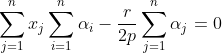
ou encore:
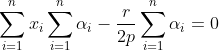
.
Donc
\bigg(\sum_{i=1}^{n}x_i-\frac{r}{2p}\bigg)=0)
. Ce qui donne
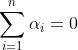
.
Par suite
: \frac{r}{2p}\alpha_j=0)
, ou bien
:\alpha_j=0)
.
D'où la liberté de la famille
)
, et la fin de la démonstration.
Sauf erreurs.
