compact

Maître Nombre de messages : 216 Age : 31 Date d'inscription : 07/03/2010

salam

soit f : A -->F une application (E et F deux evn et A [ E )

montrer que :
f continue sur tous compact de A ===> f continue sur A

?

ayoubmath a écrit:: salam
soit f : A -->F une application (E et F deux evn et A [ E )
montrer que :
f continue sur tous compact de A ===> f continue sur A?

Je propose une solution en utilisant la caractérisation séquentielle de la limite:
Supposons que $compact Gif$ est continue sur tout compact inclus dans $compact Gif$ .
Soit $compact Gif$ une suite d'éléments de $compact Gif$ convergente vers $compact Gif$ .
Il est bien connu que l'ensemble $compact N\in\mathbb{N}\}\cut\{x\}$ est compact.
Je connais une preuve de ce résultat que je n'écrirai pas, mais je renvoie à une autre différente: http://www.marocprepa.com/site/pdf/2013/article/2.pdf
On a $compact Gif$ est continue sur 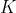$compact Gif$ , d'après l'hypothèse.
On a 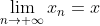$compact Gif$ et $compact Gif$ , donc $compact Gif$ .
On déduit finalement que $compact Gif$ est continue sur $compact Gif$ .
Sauf erreurs.