| | lim lnx /x en +oo |  |
|
+3Oeil_de_Lynx aymanemaysae abdelbaki.attioui 7 participants |
| Auteur | Message |
|---|
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: lim lnx /x en +oo Sujet: lim lnx /x en +oo  Sam 21 Fév 2015, 14:17 Sam 21 Fév 2015, 14:17 | |
| Donner au moins trois preuve de lnx /x -->0 quand x-->+oo
_________________
وقل ربي زد ني علما
| |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 27
Date d'inscription : 22/01/2014
 |  Sujet: Re: lim lnx /x en +oo Sujet: Re: lim lnx /x en +oo  Dim 22 Fév 2015, 18:59 Dim 22 Fév 2015, 18:59 | |
| | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 75
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: lim lnx /x en +oo Sujet: Re: lim lnx /x en +oo  Dim 22 Fév 2015, 21:21 Dim 22 Fév 2015, 21:21 | |
| BSR au Forum .
BSR Aymanmaysae .
Je passais par là ...
Je ne suis pas le correcteur de service mais je pourrais dire ce qui suit :
1ère Méthode : Tout à Fait Correcte , c'est très bien ...
" Pour tout x dans ]1;+00[ , il faut exclure la valeur 1 ....
2ème Méthode : La Règle de l' Hopital est Inopérante ICI
Revoir cette Règle et les conditions de son Application .
3ème Méthode : Tu donnes une preuve en admettant la 1ère limite
en faisant un changement de variable ...
Je Garde la 1ère Méthode , Juste à tous les points de vue .
Amicalement . LHASSANE | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 30
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: lim lnx /x en +oo Sujet: Re: lim lnx /x en +oo  Lun 23 Fév 2015, 19:55 Lun 23 Fév 2015, 19:55 | |
| - abdelbaki.attioui a écrit:
- Donner au moins trois preuve de lnx /x -->0 quand x-->+oo
J'aime bien contribuer avec cette preuve: On définit la fonction  sur 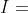 [ 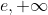 [ par : f(x)=\frac{\ln(x)}{x}) . On vérifie facilement que  : f'(x)=\frac{1}{x^2}(1-\ln(x))\le0) , donc  est décroissante. Or, on a  : f(x)\le0) donc  est minorée. Décroissante et minorée,  admet donc une limite finie qu'on note 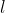 . On a }{x}=\lim_{t^2\to+\infty}\frac{\ln(t^2)}{t^2}=2\lim_{t\to+\infty}\frac{\ln(t)}{t}.\frac{1}{t}=2l\times0=0) , comme voulu. Sauf erreurs. | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 27
Date d'inscription : 22/01/2014
 |  Sujet: Re: lim lnx /x en +oo Sujet: Re: lim lnx /x en +oo  Lun 23 Fév 2015, 20:04 Lun 23 Fév 2015, 20:04 | |
| Merci pour la remarque concernant la 1ère méthode. Pour la deuxième méthode, j'ai toujours eu des problèmes avec la "Règle de l’Hôpital": j'ai essayé d'appliquer à la lettre le théorème ci-dessous, mais je crois que j'ai mal compris ce qu'il voulait dire:  Pour la troisième méthode, je vais essayer un autre chemin. Merci et Bonsoir à tous. | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 26
Date d'inscription : 23/09/2012
 |  Sujet: Re: lim lnx /x en +oo Sujet: Re: lim lnx /x en +oo  Lun 23 Fév 2015, 20:34 Lun 23 Fév 2015, 20:34 | |
| étude de la fonction f(x)=ln(x)-sqrt(x-1) sur l'intervalle [1,+oo[ nous mènera au résultat voulu.
ou un changement de variable en posant x=e^x si on veut admettre la limite de (e^x)/x comme valable.
Concernant l 'application de la règle d'Hôpital, je vois pas la condition non vérifiée. | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 26
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: lim lnx /x en +oo Sujet: Re: lim lnx /x en +oo  Mer 25 Fév 2015, 13:01 Mer 25 Fév 2015, 13:01 | |
| la règle de l'hopital concerne des limites en des points finis je pense .... | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 26
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: lim lnx /x en +oo Sujet: Re: lim lnx /x en +oo  Mer 25 Fév 2015, 13:08 Mer 25 Fév 2015, 13:08 | |
| pour un usage plus sur de la règle de l'hopital on opère un changement de variable x=tan(u)  les fonctions 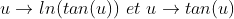 satisfaisant les conditions de l'hopital. on peut dès lors deduire que :  | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 27
Date d'inscription : 22/01/2014
 |  Sujet: Re: lim lnx /x en +oo Sujet: Re: lim lnx /x en +oo  Jeu 26 Fév 2015, 00:05 Jeu 26 Fév 2015, 00:05 | |
| | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: lim lnx /x en +oo Sujet: Re: lim lnx /x en +oo  Jeu 26 Fév 2015, 21:43 Jeu 26 Fév 2015, 21:43 | |
| | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 75
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: lim lnx /x en +oo Sujet: Re: lim lnx /x en +oo  Dim 01 Mar 2015, 20:36 Dim 01 Mar 2015, 20:36 | |
| BSR au Forum .
BSR Aymanemaysae
AUTANT POUR MOI !!!!
En effet , la Règle de l' Hospital ( 1ère Généralisation ) fonctionne .
Je n' ai jamais eu l' occasion de l' utiliser . Il faut se souvenir que cette Règle , même
dans sa version simple , n'est pas au programme du BAC Marocain SM .
Ta première méthode de l' encadrement ( Théorème des Gendarmes pour les Fonctions )
reste la MEILLEURE et la plus abordable même en BAC.....
Amicalement . LHASSANE | |
|
  | |
selfrespect
Expert sup

 Nombre de messages : 2514 Nombre de messages : 2514
Localisation : trou noir
Date d'inscription : 14/05/2006
 |  Sujet: Re: lim lnx /x en +oo Sujet: Re: lim lnx /x en +oo  Dim 01 Mar 2015, 22:31 Dim 01 Mar 2015, 22:31 | |
| Bonsoir tout le monde, Juste une précision, on ne peut pas appliquer la règle de l’hôpital pour cette limite car les contions soulignées ci-dessous ne sont pas vérifiés ( le début de cette proposition pourrait choquer certains,je m'en excuse): " Soit a réel ou égal à ±∞, tel que les fonctions réelles f et g soient définies et dérivables « au voisinage » de a, la dérivée.." (wikipédia) u -> ln(1/u) n'est pas définie au voisinage de "0" sauf si on l'étend par continuité mais ceci est une autre histoire. Pour contribuer  pi(x) est le nombre "des nombres premiers inférieur a x" clairement lim Pi(x) =+00 et cette formule permet de conclure  - Code:
-
pi(x) ~ \frac{x}{ln(x)} (c'est une blague .. ) | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 27
Date d'inscription : 22/01/2014
 |  Sujet: Re: lim lnx /x en +oo Sujet: Re: lim lnx /x en +oo  Jeu 01 Oct 2015, 15:32 Jeu 01 Oct 2015, 15:32 | |
| | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 27
Date d'inscription : 22/01/2014
 | |
  | |
Contenu sponsorisé
 |  Sujet: Re: lim lnx /x en +oo Sujet: Re: lim lnx /x en +oo  | |
| |
|
  | |
| | lim lnx /x en +oo |  |
|
