- Litorus a écrit:
- Trouver toutes les fonctions croissantes de IN-->IN
Qui vérifient : f(n+f(n))=2f(n)
Cet exercice n'est pas du tout évident. Est-ce que tu peux partager une solution ?
Sache que le problème devient trivial si on impose que

est strictement croissante.
Au passage, au lieu de considérer
=f(n)-n)
comme l'a fait nail, j'ai pensé à considérer
=f(n)+n)
.
La fonction
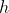
vérifie l'équation fonctionnelle
)=3h(n)-2n)
. On peut voir que
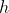
est strictement croissante et est bijective, mais cela ne nous aide pas trop. De plus, la théorie de résolution d'équations de récurrence ne nous aide pas non plus (En vrai, on aboutit au premier résultat avancé par nail).
- naïl a écrit:
- :n و m المعادلة
تستلزم لكل صحيحين طبيعيين
f[n+ (2^m- 1)f(n)] = 2^m f(n) par récurrence sur n
n |---> pE[(n+ a)/ p]+ a où p et a sont des constantes entières naturelles sont des solutions
La forme des solutions que tu trouves est plutôt la suivante:
=p\left(E\left(\frac{n}{p}\right)+a\right))
pour des entiers naturels

et

fixés.
Les fonctions constantes sont aussi solution au problème (les fonctions constantes sont croissantes au sens large).
- naïl a écrit:
- f devrait avoir les mêmes conditions que sur https://mathsmaroc.jeun.fr/t20558-quation-fonctionnelle-assez-intressante#172261, sauf qu'elle est discrete. Ce qui inclurait une solution en plus.
Je ne pense pas que ce sont les seules solutions. En cherchant sur Internet, j'ai trouvé un exercice qui ressemble à l'exercice proposé dont on peut s'inspirer: https://artofproblemsolving.com/community/c6h1604376p10001604.
Au plaisir !
