DEVOIR N 1 OLYMPIADE PREMIERE SM 24 NOVEMBRE 2017

Prob 1:
1.Le nombres des a_i qui sont impaires est 1009, et le nombres des i qui sont paires est 1008, donc il existe au moins un entier k t.q a_k-k soit paire, alors N est paire.

2.

Prob 2:

1.

2.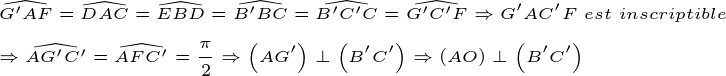



Prob 3:
Soient (C) une cercle du rayon r=1 et du centre O, supposent que O est du couleur (C1), s'il existe 2017 points du couleur (C1) appartenant a la cercle (C) alors on est terminé. Sinon on prend n points d'un arc de (C)  du longueur=1, donc pour tous les Ai points dans l'arc il existe au moins une point Bi qui appartient a la cercle (et pas l'arc) tel que AiBi=1 (il suffit de prendre Ai comme le centre d'une cercle (Ci) du rayon=1 et Bi l’intersection du (Ci) avec (C)\{arc}) donc pour les n couple (Ai,Bi) choisis il existe au maximum 2016 couple t.q l'un de (Ai ou Bi) du couleur (C1) et tous le reste sont des points du couleur (C2), alors il suffit de prendre n≥3033 pour démontrer qu'il existe au moins 2017 couple (Ai,Bi) du même couleurs (C2) avec AiBi=1.