On a :
a²b+b+a>ab²+b=>ab+1>b²=>ab+1>=b²+1
Donc :
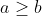
D'autre part :
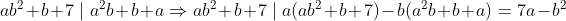 Cas 1 :
Cas 1 : a=0
Le condition s'écrit a+8|a => a=0
Cas 2 : b=0
La condition s'écrit 7|a alors le couple (7k,0) est une solution
Si a,b>0 On a les cas suivant :
Cas 3 :b²=7a
Alors 7|b² et 7|a :
Posons : b=7c ,a=7d;c²=d
La condition s'écrit :
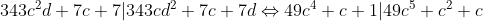
Ce qui est vrai alors le couple (7k²,7k) est une solution
Cas 4: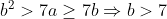
Donc ce cas on a :
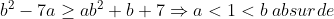 Cas 5 :
Cas 5 :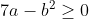
Alors on a :
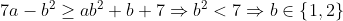
Si b=1 alors on a :
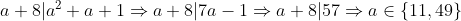
Donc les couples (11,1)et(49,1) sont des solutions .
Si b=2 alors :
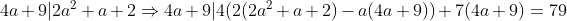
Cette dernière n'admet pas de solution .
Enfin :
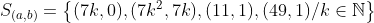
J'espère que je n'ai rien raté.

