| | exo OLYMPIADES ( 12 mars 2010 ) |  |
|
+5noirouge Sylphaen oussama1305 yassine-516 Nasslahsen 9 participants |
| Auteur | Message |
|---|
Nasslahsen
Féru

 Nombre de messages : 65 Nombre de messages : 65
Age : 32
Localisation : France
Date d'inscription : 02/01/2009
 |  Sujet: exo OLYMPIADES ( 12 mars 2010 ) Sujet: exo OLYMPIADES ( 12 mars 2010 )  Ven 12 Mar 2010, 22:33 Ven 12 Mar 2010, 22:33 | |
| Soient x; y;z ; t des nombres réels strictement positifs tel que : x+y+z+t =1
Montrer que : 6(x^3 +y^3+z^3+t^3 )>= x^2+y^2+z^2+t^2+1/8 | |
|
  | |
yassine-516
Maître

 Nombre de messages : 128 Nombre de messages : 128
Age : 31
Date d'inscription : 11/10/2009
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Ven 12 Mar 2010, 22:41 Ven 12 Mar 2010, 22:41 | |
| par Chebychev on a
x^3 +y^3+z^3+t^3 >=1/4(x^2+y^2+z^2+t^2)
donc 6(x^3 +y^3+z^3+t^3 )>=3/2(x^2+y^2+z^2+t^2)
donc il suffit de montrer que 3/2(x^2+y^2+z^2+t^2)>=x^2+y^2+z^2+t^2+1/8
ce qui est équivalent à x^2+y^2+z^2+t^2>=1/4
ce qui est vrai par c.s | |
|
  | |
Nasslahsen
Féru

 Nombre de messages : 65 Nombre de messages : 65
Age : 32
Localisation : France
Date d'inscription : 02/01/2009
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Ven 12 Mar 2010, 22:50 Ven 12 Mar 2010, 22:50 | |
| kayn a ba yassiinn ^^ 9na3tini ^^ | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Sam 13 Mar 2010, 11:42 Sam 13 Mar 2010, 11:42 | |
| - yassine-516 a écrit:
- par Chebychev on a
x^3 +y^3+z^3+t^3 >=1/4(x^2+y^2+z^2+t^2)
donc 6(x^3 +y^3+z^3+t^3 )>=3/2(x^2+y^2+z^2+t^2)
donc il suffit de montrer que 3/2(x^2+y^2+z^2+t^2)>=x^2+y^2+z^2+t^2+1/8
ce qui est équivalent à x^2+y^2+z^2+t^2>=1/4
ce qui est vrai par c.s Il y'a une méthode avec la convexité, beaucoup plus simple: Prenons [img]http://latex.codecogs.com/gif.latex?f(x) = 6x²-x On a  = 12x-1) (f est croissante sur [1/4;+infini[) et  = 12 >0) (f est convexe) D'après Jensen : + yf(y) + zf(z) + tf(t) >= f(x²+y²+z²+t²) >= f(1/4)) (d'après C-S.) Donc  >= 1/8) Et on conclue. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Sam 13 Mar 2010, 13:03 Sam 13 Mar 2010, 13:03 | |
| C'est un ancien exo d'oly de maroc ^^
Regardez ici :
http://mesex.ifrance.com/Olypiade/ghaz/test4an08_p2sol.gif | |
|
  | |
noirouge
Féru
 Nombre de messages : 54 Nombre de messages : 54
Age : 32
Date d'inscription : 29/01/2009
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Sam 13 Mar 2010, 13:27 Sam 13 Mar 2010, 13:27 | |
| Salut!
est ce un exo de l'olympiade d'hier de TSM???
mais c'est un trivial classique exercice,pourriez vous nous poster tous les exercices de votre olympiade??!!!
merci d'avance.. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Sam 13 Mar 2010, 13:43 Sam 13 Mar 2010, 13:43 | |
| Le 1er exo c'était de résoudre le système ; 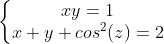 Le 2éme c'est l'inégo . 3et4 c'est le même avec les 1ér ! | |
|
  | |
noirouge
Féru
 Nombre de messages : 54 Nombre de messages : 54
Age : 32
Date d'inscription : 29/01/2009
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Sam 13 Mar 2010, 14:02 Sam 13 Mar 2010, 14:02 | |
| mais ce premier exercice est aussi trivial..... il suffit de remplacer y par 1/x dans la deuxième équation pour avoir: x²+(cos²(z)-2)x+1=0 delta=(cos²(z)-2)²-4=cos^4 (z)-4cos²(z)=cos²(z)(cos²(z)-4)=<0 (car cos(z)=<1<2) alors cos(z)=0 ===>z=pi/2 [k pi] ==>x=y=1.... mais leur olympiade est plus trivial que celui des premières  | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Sam 13 Mar 2010, 16:20 Sam 13 Mar 2010, 16:20 | |
| Oué ^^
il suffit aussi de remarque que :
|x+1/x|>=2
Puis faire les cas x<>0 | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Sam 13 Mar 2010, 16:42 Sam 13 Mar 2010, 16:42 | |
| - Sylphaen a écrit:
- Oué ^^
il suffit aussi de remarque que :
|x+1/x|>=2
Puis faire les cas x<>0 On prouve d'abord par l'absurde que x et y sont strictement positifs, ça va faciliter. Et ceci dit, il était TRES facile, à mon avis, j'ai fais les trois premiers en une demi-heure à peu près, mais géométrie j'ai essayé mais j'ai pas trouvé. La géométrie n'est pas du tout mon fort, en passant  . | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Sam 13 Mar 2010, 17:14 Sam 13 Mar 2010, 17:14 | |
| Une autre solution pour le premier exercice. Exercice 1 :%3C%201\Rightarrow%20x+y%3E%201) Et puisque 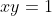 , il vient que x et y sont tout deux positifs. Ensuite, il est connu que ^2\geq%204xy=4) , d'où 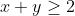 puisque x+y est positif. Ainsi, 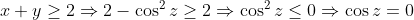 De ce fait, 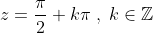 Et le système devient trivial :  Et a pour unique solution le couple (1,1). | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Sam 13 Mar 2010, 18:42 Sam 13 Mar 2010, 18:42 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Sam 13 Mar 2010, 19:22 Sam 13 Mar 2010, 19:22 | |
| - oussama1305 a écrit:
J'ai une troisième solution.
Indice : se rappeller que 
Le reste est trivial. Joli ! | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Sam 13 Mar 2010, 20:07 Sam 13 Mar 2010, 20:07 | |
| - Dijkschneier a écrit:
- oussama1305 a écrit:
J'ai une troisième solution.
Indice : se rappeller que 
Le reste est trivial. Joli ! Merci. | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Sam 13 Mar 2010, 21:34 Sam 13 Mar 2010, 21:34 | |
| L'inégalité qu'on vous a proposé est trivial pour un TST de TSM, elle aussi deja proposé dans un autre TST. des élèves l'ont fait lorsqu'ils était au 4-ième annés collège.je vous conseille de vous entrainer sur les inégalité du level un peu plus elevé, j'en propose une,Problem (MohE):Soit  et et 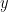 deux réels dont le produit est deux réels dont le produit est  , Prouver que: , Prouver que:  et aussi une deuxième qui est plus facile, trouvé par un ami:Problem (Alexandrescu):Soit a,b et c trois réels non-négative tels que, a^3b^3+b^3c^3+c^3a^3+2a^3b^3c^3=1.trouver le minimum de l'expression A=a²+b²+c² Bonne chance pour l'IMO et pour resoudre ces deux exos.P.S: si quelqu'un a la copie du 3-ième et 4-ième TST, en format PDF, ou Image, ou quelque chose du genre, qu'il me les envoies par mp svp, et merci d'avance. et aussi une deuxième qui est plus facile, trouvé par un ami:Problem (Alexandrescu):Soit a,b et c trois réels non-négative tels que, a^3b^3+b^3c^3+c^3a^3+2a^3b^3c^3=1.trouver le minimum de l'expression A=a²+b²+c² Bonne chance pour l'IMO et pour resoudre ces deux exos.P.S: si quelqu'un a la copie du 3-ième et 4-ième TST, en format PDF, ou Image, ou quelque chose du genre, qu'il me les envoies par mp svp, et merci d'avance. | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Dim 14 Mar 2010, 12:55 Dim 14 Mar 2010, 12:55 | |
| delted
faute de concavité!
Dernière édition par houssam110 le Dim 14 Mar 2010, 19:57, édité 5 fois (Raison : déterminer le cas dégalité) | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Dim 14 Mar 2010, 13:09 Dim 14 Mar 2010, 13:09 | |
| | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Dim 14 Mar 2010, 13:20 Dim 14 Mar 2010, 13:20 | |
|
Dernière édition par houssam110 le Dim 14 Mar 2010, 19:58, édité 2 fois | |
|
  | |
.
Maître
 Nombre de messages : 296 Nombre de messages : 296
Age : 33
Localisation : Maroc.
Date d'inscription : 18/08/2009
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  Dim 14 Mar 2010, 16:14 Dim 14 Mar 2010, 16:14 | |
| non cette fonction n'est pas concave sur IR+ | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: exo OLYMPIADES ( 12 mars 2010 ) Sujet: Re: exo OLYMPIADES ( 12 mars 2010 )  | |
| |
|
  | |
| | exo OLYMPIADES ( 12 mars 2010 ) |  |
|
