| | 1exo abordale et 1autre 1/2 abordale |  |
|
|
| Auteur | Message |
|---|
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: 1exo abordale et 1autre 1/2 abordale Sujet: 1exo abordale et 1autre 1/2 abordale  Jeu 16 Oct 2008, 18:23 Jeu 16 Oct 2008, 18:23 | |
| | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: 1exo abordale et 1autre 1/2 abordale Sujet: Re: 1exo abordale et 1autre 1/2 abordale  Jeu 16 Oct 2008, 18:31 Jeu 16 Oct 2008, 18:31 | |
| - madani a écrit:
 BSR Mr MADANI !!! Pour la deuxième , la majoration de la somme par (3/2) me parait fausse de toute évidence ; prendre n=1 par exemple pour s'en convaincre !! A moins d'écarter cette valeur parasite , auquel cas : pour tout i=0,1,.............,n on a n<=n+i<=2n d'ou 1/(n+i) <=1/n d'ou ta SOMME <=(n+1)/n=1+(1/n) et comme n>=2 alors (1/n)<=1/2 et puis on finalise 1+(1/n)<=3/2 EN CONCLUSION : ton encadrement est vrai si n est dans IN\{0;1} | |
|
  | |
Koutaiba
Expert grade2
 Nombre de messages : 396 Nombre de messages : 396
Age : 32
Localisation : Rabat
Date d'inscription : 04/08/2008
 |  Sujet: Re: 1exo abordale et 1autre 1/2 abordale Sujet: Re: 1exo abordale et 1autre 1/2 abordale  Jeu 16 Oct 2008, 19:36 Jeu 16 Oct 2008, 19:36 | |
| Salut
pour la 1ére question
on verifie 2 >= 1
on suppose que 2^n >= n^2
on demontre que
2^(n + 1) >= (n + 1) ^2
on a
2^n >= n^2
2^(n + 1) >= 2n^2
alors il faut montrer que
2n^2 >= n^2 + 2n + 1
n^2 - 2n - 1 >= 0
cad
n(n-2) - 1 >= 0
on sait que n>=4
n(n-2) >=8
n(n-2) - 1 >= 7
donc
n(n-2) - 1 > 0
alors
2^(n + 1) >= (n + 1) ^2
conclusion
A n appartient à IN sauf 1,2,3 on a 2^n >= n^2 | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: 1exo abordale et 1autre 1/2 abordale Sujet: Re: 1exo abordale et 1autre 1/2 abordale  Jeu 16 Oct 2008, 20:01 Jeu 16 Oct 2008, 20:01 | |
| - Oeil_de_Lynx a écrit:
- madani a écrit:

BSR Mr MADANI !!!
Pour la deuxième , la majoration de la somme par (3/2) me parait fausse de toute évidence ; prendre n=1 par exemple pour s'en convaincre !!
A moins d'écarter cette valeur parasite , auquel cas :
pour tout i=0,1,.............,n on a n<=n+i<=2n
d'ou 1/(n+i) <=1/n
d'ou ta SOMME <=(n+1)/n=1+(1/n) et comme n>=2 alors (1/n)<=1/2 et puis on finalise 1+(1/n)<=3/2
EN CONCLUSION : ton encadrement est vrai si n est dans IN\{0;1}
BSR prof effectivt on doit avoir n>1 mais pour les demonstrations par reccurence les eleves ont l'habitude a ce genre d'erreur et d'ailleur cé 1 exo du livre scolaire contrairement au 1ere! | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: 1exo abordale et 1autre 1/2 abordale Sujet: Re: 1exo abordale et 1autre 1/2 abordale  Jeu 23 Oct 2008, 18:31 Jeu 23 Oct 2008, 18:31 | |
| BSR
je donne d'abord une solution pour :1/2<1/(1+n)+.....+1/2n
on a:
1/(1+n)>1/2n
1/(2+n)>1/2n
.
.
.
1/2n >=1/2n
en faisant la somme membre a membre on obtient:
1/(1+n)+.....+1/2n >1/2 | |
|
  | |
Koutaiba
Expert grade2
 Nombre de messages : 396 Nombre de messages : 396
Age : 32
Localisation : Rabat
Date d'inscription : 04/08/2008
 |  Sujet: Re: 1exo abordale et 1autre 1/2 abordale Sujet: Re: 1exo abordale et 1autre 1/2 abordale  Sam 25 Oct 2008, 16:33 Sam 25 Oct 2008, 16:33 | |
| salut !!!
de la méme façon on a
1/(1+n)< 3/2n
1/(2+n)< 3/2n
.
.
.
1/2n < 1/2n
en faisant la somme membre a membre on obtient:
1/(1+n)+.....+1/2n < 3/2
mais je crois qu'il faut résoudre l'exo par réccurence ... | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: 1exo abordale et 1autre 1/2 abordale Sujet: Re: 1exo abordale et 1autre 1/2 abordale  Dim 26 Oct 2008, 11:39 Dim 26 Oct 2008, 11:39 | |
| - Koutaiba a écrit:
- salut !!!
de la méme façon on a
1/(1+n)< 3/2n
1/(2+n)< 3/2n
.
.
.
1/2n < 1/2n
en faisant la somme membre a membre on obtient:
1/(1+n)+.....+1/2n < 3/2
mais je crois qu'il faut résoudre l'exo par réccurence ... ta raison !je me suis trompé d'exo generalement on ne doix ps utiliser la reccurence que si d autre methodes plus simples st impuissants! 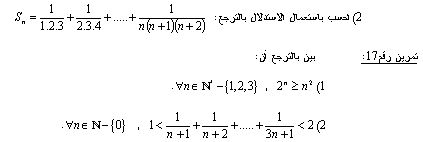 | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: 1exo abordale et 1autre 1/2 abordale Sujet: Re: 1exo abordale et 1autre 1/2 abordale  Mer 12 Nov 2008, 17:17 Mer 12 Nov 2008, 17:17 | |
| bsr je donne la slt pour la derniere question:  | |
|
  | |
miss-Design
Expert grade2

 Nombre de messages : 337 Nombre de messages : 337
Age : 32
Localisation : Agadir
Date d'inscription : 25/10/2008
 |  Sujet: Re: 1exo abordale et 1autre 1/2 abordale Sujet: Re: 1exo abordale et 1autre 1/2 abordale  Mer 12 Nov 2008, 18:05 Mer 12 Nov 2008, 18:05 | |
| pour cet exercice nous l'avons déjà fait au Tc premièrement :  | |
|
  | |
miss-Design
Expert grade2

 Nombre de messages : 337 Nombre de messages : 337
Age : 32
Localisation : Agadir
Date d'inscription : 25/10/2008
 |  Sujet: Re: 1exo abordale et 1autre 1/2 abordale Sujet: Re: 1exo abordale et 1autre 1/2 abordale  Mer 12 Nov 2008, 18:13 Mer 12 Nov 2008, 18:13 | |
| et la deuxième inégalité :  sauf s'il y a une faute bon pour la 1ère vous avez demandé seulement 3/2 et j'ai trouvé 3/4 | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: 1exo abordale et 1autre 1/2 abordale Sujet: Re: 1exo abordale et 1autre 1/2 abordale  Mer 12 Nov 2008, 22:05 Mer 12 Nov 2008, 22:05 | |
| - miss-Design a écrit:
- et la deuxième inégalité :

sauf s'il y a une faute
bon pour la 1ère vous avez demandé seulement 3/2 et j'ai trouvé 3/4 avt de repondre a un exo je croix qu il vt mieux de lire le topic de a à z !!! | |
|
  | |
miss-Design
Expert grade2

 Nombre de messages : 337 Nombre de messages : 337
Age : 32
Localisation : Agadir
Date d'inscription : 25/10/2008
 |  Sujet: Re: 1exo abordale et 1autre 1/2 abordale Sujet: Re: 1exo abordale et 1autre 1/2 abordale  Jeu 13 Nov 2008, 11:52 Jeu 13 Nov 2008, 11:52 | |
| bon je m'excuse !!
même si la solution est postée on peut avoir la même n'est ce pas ?? | |
|
  | |
madani
Expert grade2

 Nombre de messages : 397 Nombre de messages : 397
Age : 64
Localisation : maroc-salé
Date d'inscription : 08/09/2007
 |  Sujet: Re: 1exo abordale et 1autre 1/2 abordale Sujet: Re: 1exo abordale et 1autre 1/2 abordale  Jeu 13 Nov 2008, 16:17 Jeu 13 Nov 2008, 16:17 | |
| - miss-Design a écrit:
- bon je m'excuse !!
même si la solution est postée on peut avoir la même n'est ce pas ?? 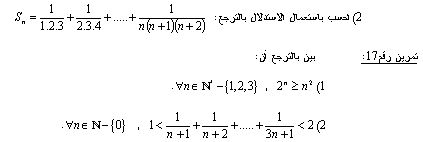 ce que tu as fait est bon puisque tu as presenté une methode differente mais on aurait b1 aimé que ça soit pour l exo en question !!!(le2 du 17) | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: 1exo abordale et 1autre 1/2 abordale Sujet: Re: 1exo abordale et 1autre 1/2 abordale  | |
| |
|
  | |
| | 1exo abordale et 1autre 1/2 abordale |  |
|
