| | a.b -de IR+ |  |
|
|
| Auteur | Message |
|---|
kirua
Expert sup

 Nombre de messages : 647 Nombre de messages : 647
Age : 31
Date d'inscription : 03/10/2008
 |  Sujet: a.b -de IR+ Sujet: a.b -de IR+  Sam 22 Nov 2008, 10:01 Sam 22 Nov 2008, 10:01 | |
| salut ^^ voici un exo po tro difficile : bon en a : a et b de IR^+ demontre que 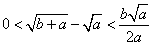 | |
|
  | |
kirua
Expert sup

 Nombre de messages : 647 Nombre de messages : 647
Age : 31
Date d'inscription : 03/10/2008
 |  Sujet: Re: a.b -de IR+ Sujet: Re: a.b -de IR+  Sam 22 Nov 2008, 10:04 Sam 22 Nov 2008, 10:04 | |
| un autre exo ohsob E
E=1000²-999²+998²-997²+.....+4²-3²+2²-1² | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: a.b -de IR+ Sujet: Re: a.b -de IR+  Sam 22 Nov 2008, 12:23 Sam 22 Nov 2008, 12:23 | |
| soit f(x) = rac(x+a) définie pour x >= 0 et a > 0
appliquer les inégalités ses accroissements finis
en remarquant que f'(x) = 1/2rac(x+a)
donc 0 < f'(x) < 1/2rac(a)
0 < f(b) - f(0) < (b - 0) . 1/2rac(a)
0 < rac(b+a) - rac(a) < b.rac(a) / 2a | |
|
  | |
HMXXMH
Expert sup

 Nombre de messages : 748 Nombre de messages : 748
Age : 32
Localisation : chez moi
Date d'inscription : 08/10/2008
 |  Sujet: Re: a.b -de IR+ Sujet: Re: a.b -de IR+  Sam 22 Nov 2008, 12:24 Sam 22 Nov 2008, 12:24 | |
| | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: a.b -de IR+ Sujet: Re: a.b -de IR+  Sam 22 Nov 2008, 12:28 Sam 22 Nov 2008, 12:28 | |
| | |
|
  | |
samia08
Maître
 Nombre de messages : 122 Nombre de messages : 122
Age : 30
Date d'inscription : 26/09/2008
 |  Sujet: Re: a.b -de IR+ Sujet: Re: a.b -de IR+  Sam 22 Nov 2008, 19:30 Sam 22 Nov 2008, 19:30 | |
| salut voila la reponse du 2eme exo
E=1000²-999²+998²-997²+.....+4²-3²+2²-1²
E=1*(1000+999)+1*(998+997)..........+1*(4+3)+1*(1+2)
E=1+2+3+4..............997+998+999+1000
E=500.5-499.5+500.5-498.5+..........500.5+498.5+500.5+499.5
E=500.5*1000
E=5.0005*10^5
es juste? | |
|
  | |
HMXXMH
Expert sup

 Nombre de messages : 748 Nombre de messages : 748
Age : 32
Localisation : chez moi
Date d'inscription : 08/10/2008
 |  Sujet: Re: a.b -de IR+ Sujet: Re: a.b -de IR+  Sam 22 Nov 2008, 19:42 Sam 22 Nov 2008, 19:42 | |
| | |
|
  | |
samia08
Maître
 Nombre de messages : 122 Nombre de messages : 122
Age : 30
Date d'inscription : 26/09/2008
 |  Sujet: Re: a.b -de IR+ Sujet: Re: a.b -de IR+  Sam 22 Nov 2008, 19:56 Sam 22 Nov 2008, 19:56 | |
| derien,stp poste d'autres exos
amicalemaent | |
|
  | |
kirua
Expert sup

 Nombre de messages : 647 Nombre de messages : 647
Age : 31
Date d'inscription : 03/10/2008
 |  Sujet: Re: a.b -de IR+ Sujet: Re: a.b -de IR+  Sam 22 Nov 2008, 20:37 Sam 22 Nov 2008, 20:37 | |
| - houssa a écrit:
- soit f(x) = rac(x+a) définie pour x >= 0 et a > 0
appliquer les inégalités ses accroissements finis
en remarquant que f'(x) = 1/2rac(x+a)
donc 0 < f'(x) < 1/2rac(a)
0 < f(b) - f(0) < (b - 0) . 1/2rac(a)
0 < rac(b+a) - rac(a) < b.rac(a) / 2a po bien pige | |
|
  | |
kirua
Expert sup

 Nombre de messages : 647 Nombre de messages : 647
Age : 31
Date d'inscription : 03/10/2008
 |  Sujet: Re: a.b -de IR+ Sujet: Re: a.b -de IR+  Sam 22 Nov 2008, 20:38 Sam 22 Nov 2008, 20:38 | |
| n utilise po al dawal pls moi j ai trouvai la reponsse mais je veus voir les votre | |
|
  | |
girl-ambition.93
Maître

 Nombre de messages : 195 Nombre de messages : 195
Age : 31
Date d'inscription : 03/07/2008
 |  Sujet: Re: a.b -de IR+ Sujet: Re: a.b -de IR+  Sam 22 Nov 2008, 21:14 Sam 22 Nov 2008, 21:14 | |
| j'ai po compris ta reponse samia08!!
j'ai trouve 4004!! | |
|
  | |
girl-ambition.93
Maître

 Nombre de messages : 195 Nombre de messages : 195
Age : 31
Date d'inscription : 03/07/2008
 |  Sujet: Re: a.b -de IR+ Sujet: Re: a.b -de IR+  Sam 22 Nov 2008, 21:16 Sam 22 Nov 2008, 21:16 | |
| ah oui c tres claire dsl samia08
ce ke je vx dire si il en a une autre methode!! | |
|
  | |
samia08
Maître
 Nombre de messages : 122 Nombre de messages : 122
Age : 30
Date d'inscription : 26/09/2008
 |  Sujet: Re: a.b -de IR+ Sujet: Re: a.b -de IR+  Sam 22 Nov 2008, 21:33 Sam 22 Nov 2008, 21:33 | |
| voila une regle generale
que j'ai deduit
1+2+3+4..............+n-1+n=((n+1)/2)*n
exemple
1+2+3+4+5=((5+1)/2)*5=15
bonne chance et bonne continueté | |
|
  | |
girl-ambition.93
Maître

 Nombre de messages : 195 Nombre de messages : 195
Age : 31
Date d'inscription : 03/07/2008
 |  Sujet: Re: a.b -de IR+ Sujet: Re: a.b -de IR+  Sam 22 Nov 2008, 21:47 Sam 22 Nov 2008, 21:47 | |
| ah oui je l'ai oublie mrc bcp!! | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: a.b -de IR+ Sujet: Re: a.b -de IR+  | |
| |
|
  | |
| | a.b -de IR+ |  |
|
