olympiade

salut.

bon lecture! et n'oubliez pas de poster vos solution et sans aucun theoreme.

Merci mathsmaster:

Bonjour

Exercice 2:

1)On a: a³+b³+c³-3abc= 1\2(a+b+c)((a-b)²+(b-c)²+(c-a)²)

Puisque: (a+b+c)((a-b)²+(b-c)²+(c-a)²)≥0

Donc a³+b³+c³≥3abc

2)

On a a²+1\b + b²+1\c +c²+1\a>= 2(a\b+b\c+c\a) >= 2.3 =6 (d'apres 1 question)

slt !!
pour l'exo 1:

C'est ce que j'ai fait^^

Mais je penses qu'on a commis une faute 3 est l'autre solution

Oui , 3 est une solution , si on fait (V[2-V(x+1)] on va trouver que x=3
^^

pour le premier exo je crois que c facile car on a fais le truc dans 2 eme annee college

il ya 4 solution

x=3 et x=8 et 1=1 et 1=1

xyzakaria a écrit:

pour le premier exo je crois que c facile car on a fais le truc dans 2 eme annee college

il ya 4 solution

x=3 et x=8 et 1=1 et 1=1

?????

hé les amis vous avez commis des fautes, une fois arrivé a:
|V(x+1)-2|+|V(x+1)-3|=1.
la il faut faire une disjonction de cas:
V(x+1)=<2 , 2<V(x+1)=<3, V(x+1)>3
...

note: exo1 et exo 3 sont pris du livre (annaja7) les deux autres c autre chose.

ex 1 :

pour ce genre d'exercice mieux de choisir un autre inconnu :

O = V(x+1)

V(O^2 -4O +4) + V(O^2-6O + 9) =1 {====}
(O-2)+(0-3) =1 {====}
O = 3
donc x = 8

topmath a écrit:

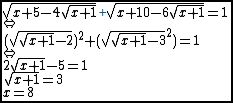mes congratulations pour découvrir que les nombres dans les racines sont des carrés mais quelqu'un d'autre peut-être ne peut pas remarquer ça.

Meuh non ^^" jsuis en 3eme année collège et jlai remarqué ^^" c'est facile dès que tu vois qu'il y a un multiple de 2 x la racine d'un inconnu et que tu trouve l'inconnu aussi faut penser à l'identité =P

{}{}=l'infini a écrit:

ex 1 :

pour ce genre d'exercice mieux de choisir un autre inconnu :

O = V(x+1)

V(O^2 -4O +4) + V(O^2-6O + 9) =1 {====}
(O-2)+(0-3) =1 {====}
O = 3
donc x = 8

C faux hhhhhhhh tu dois trouver majal [3;8]
Exo 2 2)g pas utilisé(am-gm) la 1ere question et g pas compris la solution de topmath(amicalement).
Exo 3: je l'ai fait à la maison et je trouve pas -1 lorsque je remplace^^'
Exo 4 déja posté.
A+

{}{}=l'infini a écrit:

topmath a écrit:

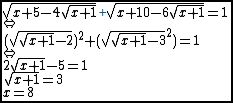
mes congratulations pour découvrir que les nombres dans les racines sont des carrés mais quelqu'un d'autre peut-être ne peut pas remarquer ça.

Je vois que t vraiment prétentieux mais lorsqu'on voit ta soluce on eclate de rire.

red11 a écrit:

{}{}=l'infini a écrit:

ex 1 :

pour ce genre d'exercice mieux de choisir un autre inconnu :

O = V(x+1)

V(O^2 -4O +4) + V(O^2-6O + 9) =1 {====}
(O-2)+(0-3) =1 {====}
O = 3
donc x = 8

C faux hhhhhhhh tu dois trouver majal [3;8]
Exo 2 2)g pas utilisé(am-gm) la 1ere question et g pas compris la solution de topmath(amicalement).
Exo 3: je l'ai fait à la maison et je trouve pas -1 lorsque je remplace^^'
Exo 4 déja posté.
A+

salut red 11,
exo2) wi il ne faut pas utiliser AM-GM. la deuxieme question.
sum{(a²+1)/b}>=sum{2a/b}=2sum{a/b}
on posons x^3=a/b y^3=b/c z^3=c/a
d'apres la premiere question. sum{a/b}>=3, d'ou ...
exo3). dsl mais l'exo est tout a fait juste et il faut la trouve, essaie encore.
exo4). soit sur qu'il n'est jamais posté, mais seulment kaychbeh lih.
j'espere que tu m'as compris.

jusqu'a present personne n'as donné une solution correct du premier exo.

mathsmaster a écrit:

red11 a écrit:

{}{}=l'infini a écrit:

ex 1 :

pour ce genre d'exercice mieux de choisir un autre inconnu :

O = V(x+1)

V(O^2 -4O +4) + V(O^2-6O + 9) =1 {====}
(O-2)+(0-3) =1 {====}
O = 3
donc x = 8

C faux hhhhhhhh tu dois trouver majal [3;8]
Exo 2 2)g pas utilisé(am-gm) la 1ere question et g pas compris la solution de topmath(amicalement).
Exo 3: je l'ai fait à la maison et je trouve pas -1 lorsque je remplace^^'
Exo 4 déja posté.
A+

salut red 11,
exo2) wi il ne faut pas utiliser AM-GM. la deuxieme question.
sum{(a²+1)/b}>=sum{2a/b}=2sum{a/b}
on posons x^3=a/b y^3=b/c z^3=c/a
d'apres la premiere question. sum{a/b}>=3, d'ou ...
exo3). dsl mais l'exo est tout a fait juste et il faut la trouve, essaie encore.
exo4). soit sur qu'il n'est jamais posté, mais seulment kaychbeh lih.
j'espere que tu m'as compris.

jusqu'a present personne n'as donné une solution correct du premier exo.

Lmajal que g donné est la réponse juste wa bayna ta dire tableau...

sans faire aucun tableau.
il faut faire un disjonction de cas.
V(x+1)=<2 ;2<V(x+1)=<3 ;V(x+1)>3

salut

je voudrais bien intervenir pour exo 3

remarquer d'abord:

x < 0
y > 1
0 < z < 1

---------------------
thalès : MB/MC = AB/AP = AN/AC (tout en distance)

MB/MC= -x

AB/AP = (PB-AP)/AP = (1/z.AP - AP)/AP = 1/z - 1

AN/AC = AN/(NC-AN) = AN/(y.AN -AN) = 1/(y-1)
-------------------------------------------------------------

Donc: -x = 1/z - 1 = 1/(y-1)

y=(x-1)/x et z = 1/(1-x)

on vérifie : xyz = -1
----------------------------------------

pour exo 4:

on pose : P(x) = a.X^n +..............
( aX^n :le terme du plus haut degré) tphd)

le( tphd) de gauche est : a.3^n.X^(n+1) + ..........
le (tphd) de droite est : 81.a.X^(n+1) + .......

donc : 3^n = 81 ====>n=4

P(X) = aX^4 + bX^3 + cX^2 + dX + e

on remplace P(X) et P(3X)

par identification:

81(b-a) = 27b - 81^2.a
etc......

pour exo4. apres avoir trouver que P est du 4eme degré. mieux de prendre P(x)=(x-a)(x-b)(x-c)(x-d) tu vas pas bcp calculer.

red11 a écrit:

{}{}=l'infini a écrit:

topmath a écrit:

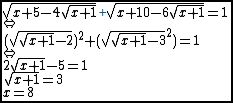
mes congratulations pour découvrir que les nombres dans les racines sont des carrés mais quelqu'un d'autre peut-être ne peut pas remarquer ça.

Je vois que t vraiment prétentieux mais lorsqu'on voit ta soluce on eclate de rire.

si tu vois que ma réponse est fausse ça ne dit que je suis prétentieux et je ne trouve pas la prétention à mon deuxième message
j'ai parlé avec topmaths onta machi so9ek
geltlih dik lhadra 7int ana ma la7edtch chno la7ed howa tbarklah 3lih
j'ai cryé que j'ai donné une méthode plus facile que l'on peu appliquer à tous les exercices de genre pareil "choisir un nouveau inconnu"

mas7abtch a "red 11" ghat bda t3ayrni
yaak achno dert lik
mais ana ma ghan 3ayrekch menek lah ...

pr le premier exercice il y a trois solutions pour faciliter dirou jadwal l ichara x=8 ou x=3 1=1