| | pour les amteurs de "caushy" |  |
|
|
| Auteur | Message |
|---|
{}{}=l'infini
Expert sup
 Nombre de messages : 1164
Age : 32
Date d'inscription : 25/09/2008
| | Sujet: pour les amteurs de "caushy" Mer 11 Fév 2009, 16:41 | |
| on a : a+b+c+d+e = 8 et a²+b²+c²+d²+e² = 16 donner la valeur maximale de c . ( USA ) c pas très difficile ..  allez bon courage , et félicitation pour vos notes !!  | |
|
| | |
anass-sci
Maître
Nombre de messages : 128
Age : 31
Date d'inscription : 29/01/2009
| | Sujet: Re: pour les amteurs de "caushy" Mer 11 Fév 2009, 16:55 | |
| bonjour !!
d'après Cauchy on a :
( a +b +c + d )² =< ( 1 +1 +1 +1 ) ( a²+b² + c² + d² ) = 4 ( a²+b²...) nous donnes ( 8 - e ) ² =< 4 ( 16 - e²)
veut dire que : e ( 5e-16) =< 0
0 =< e =< 16/5
.........................
si j'ai pas fais des fautes de calcul nous aurons c = 6/5
*****quelqu'un complète !!
**j'ai déjà travaillé cet exo !! | |
|
| | |
anass-sci
Maître
Nombre de messages : 128
Age : 31
Date d'inscription : 29/01/2009
| | Sujet: Re: pour les amteurs de "caushy" Mer 11 Fév 2009, 20:30 | |
| | |
|
| | |
xyzakaria
Expert grade2
Nombre de messages : 374
Age : 31
Date d'inscription : 12/12/2008
| | Sujet: Re: pour les amteurs de "caushy" Jeu 12 Fév 2009, 13:57 | |
| | |
|
| | |
legend-crush
Expert sup
Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
| | Sujet: Re: pour les amteurs de "caushy" Sam 30 Mar 2013, 15:35 | |
| je l'ai trouvé dans le livre de Pierre borneitz sur les inegalités!! | |
|
| | |
jlibene
Habitué
Nombre de messages : 12
Age : 26
Localisation : alabasta
Date d'inscription : 17/10/2012
| | Sujet: Re: pour les amteurs de "caushy" Sam 20 Avr 2013, 11:42 | |
| Je ne connais pas ce "Caushy" dont vous parlez ni ce "Pierre borneitz" mais jai pu demontrer ca : - Spoiler:
- Montrer que les inconnus sont positifs :On suppose que : e < 0 *on aura a+b+c+d>8 -4a-4b-4c-4d<-32 *on aura aussi a²+b²+c²+d²<16 alors a²-4a+b²-4b+c²-4c+d²-4d<-16 a²-4a+4+b²-4b+4+c²-4c+4+d²-4d+4<0 (a-2)²+(b-2)²+(c-2)²+(d-2)²<0 (WTF ??!  ) donc e est positif on fait de meme pour tous les autres donc a,b,c,d et e >=0-Trouver le maximumpour que c soit maximale, il faut que a, b, d et e soient minimales. et le minimum pour eux, c'est 0 *on prend e = 0 a²+b²+c²+d² = 16 a²-4a+4+b²-4b+4+c²-4c+4+d²-4d+4 = 0 (a-2)²+(b-2)²+(c-2)²+(d-2)² = 0 alors lunique solution dans ce cas serait (2,2,2,2,0) DONC LE MAXIMUM DE C EST 2!!!
S'il y a faute je vous prie de corriger et merci | |
|
| | |
legend-crush
Expert sup
Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
| | Sujet: Re: pour les amteurs de "caushy" Sam 20 Avr 2013, 12:38 | |
| voila l'inegalité de caushy schwarz:  eten l'utilisant tu peux facilement trouver la solution!!
Dernière édition par legend-crush le Sam 20 Avr 2013, 12:49, édité 1 fois | |
|
| | |
legend-crush
Expert sup
Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
| | Sujet: Re: pour les amteurs de "caushy" Sam 20 Avr 2013, 12:48 | |
| Je reprends ce que Anass-sci a deja écrit :  | |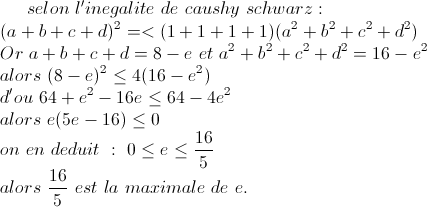
|
| | |
jlibene
Habitué
Nombre de messages : 12
Age : 26
Localisation : alabasta
Date d'inscription : 17/10/2012
| | Sujet: Re: pour les amteurs de "caushy" Sam 20 Avr 2013, 17:31 | |
| euh...si tu le dis...  mais je crois que e <= 16/5 ne veut pas dire obligatoirement que 16/5 est la valeur maximale de e, ca voudrait dire plutot que la maximale ne depasse pas 16/5 , sinon il faut aussi que 16/5 soit une valeur possible pour e(si cest le cas tu pourrais mettre les valeurs des autres inconnus stp  ?). Dans ce cas, si on suit ce raisonnement , moi aussi je dirais :  ............... : mode délire ~ on:............... a²+b²+c²+d²+e²=16 e²<=16 e<=4 donc 4 est la valeur maximale nyanyanya  ............... : mode délire ~ off:............... | |
|
| | |
Humber
Expert grade2
Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
| | Sujet: Re: pour les amteurs de "caushy" Sam 20 Avr 2013, 19:35 | |
| - jlibene a écrit:
- e <= 16/5 ne veut pas dire obligatoirement que 16/5 est la valeur maximale de e, ca voudrait dire plutot que la maximale ne depasse pas 16/5
. Cool ça. Si 0<=e <= a , alors e peut avoir n'importe quel valeur dans [0,a]. La valeur maximale qu'elle peut prendre c'est le plus grand nombre dans cet intervalle, qui est ? | |
|
| | |
jlibene
Habitué
Nombre de messages : 12
Age : 26
Localisation : alabasta
Date d'inscription : 17/10/2012
| | Sujet: Re: pour les amteurs de "caushy" Dim 21 Avr 2013, 10:53 | |
| Comment tu sais que e prend nimporte quelle valeur dans lintervalle [0,16/5] Je crois quil faudrait demontrer que 16/5 est une valeur possible : - Spoiler:
- si e = 16/5 :
{a+b+c+d= 4.8
{a²+b²+c²+d²= 5.76
a²+b²+c²+d² = 5.76
a²+b²+c²+d² = (4.8 )²/4
a²+b²+c²+d² = (a+b+c+d)²/4
4a²+4b²+4c²+4d² = a²+b²+c²+d²+2ab+2ac+2ad+2bc+2bd+2cd
3a²+3b²+3c²+3d²-2ab-2ac-2ad-2bc-2bd-2cd=0
(a-b)²+(a-c)²+(a-d)²+(b-c)²+(b-d)²+(c-d)²=0
alors :
a=b=c=d
4a = 4.8
a = 1.2
de meme pour b et c et d
| |
|
| | |
legend-crush
Expert sup
Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
| | Sujet: Re: pour les amteurs de "caushy" Mer 24 Avr 2013, 19:53 | |
| - jlibene a écrit:
sinon il faut aussi que 16/5 soit une valeur possible pour e
Wé Wé la je suis dacord avec toi  , même si dans la démo, ceci est très bien pris en compte ( quand on remplace a+b+c+d par 8-e et a²+b²+c²+d² par 16-e, ça montre que e remplis bien les deux données) Amicalement, | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: pour les amteurs de "caushy" | |
| |
|
| | |
| | pour les amteurs de "caushy" | |
|
