| | toc toc toc! olympiades |  |
|
|
| Auteur | Message |
|---|
mouad01
Maître
 Nombre de messages : 271
Age : 32
Localisation : dans la lune ou sur le nuage qui me transporte
Date d'inscription : 12/04/2008
| | Sujet: toc toc toc! olympiades Dim 22 Mar 2009, 00:09 | |
| Créteil
Quelles sont les solutions de cette équation ? Expliquez.
x=1+ 1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/X))))))))))
Désolé jé beau essayé pr limage sa na pa marché | |
|
| | |
milor18
Maître
Nombre de messages : 153
Age : 31
Localisation : fes
Date d'inscription : 23/12/2007
| | Sujet: Re: toc toc toc! olympiades Dim 22 Mar 2009, 10:11 | |
| l'equation équivaut à : X=1+1/X il s'agit d'une équation de second degré dont les racines sont : x = (1+V5)/2 et (1-V5)/2 et comme x>0 : x= (1+V5)/2 = le nombre d'or  | |
|
| | |
mouad01
Maître
Nombre de messages : 271
Age : 32
Localisation : dans la lune ou sur le nuage qui me transporte
Date d'inscription : 12/04/2008
| | Sujet: Re: toc toc toc! olympiades Dim 22 Mar 2009, 10:22 | |
| comment savoir que
l'equation équivaut à : X=1+1/X | |
|
| | |
milor18
Maître
Nombre de messages : 153
Age : 31
Localisation : fes
Date d'inscription : 23/12/2007
| | Sujet: Re: toc toc toc! olympiades Dim 22 Mar 2009, 10:29 | |
| en fait, cette équation tend vers l'infini ( c'est à dire une infinité de fractions ) on peut donc écrire X= 1+1/X ( remarque que le dénominateur du deuxième "1" est égale au X ) j'espère que c assez clair !! | |
|
| | |
Rabab
Habitué
 Nombre de messages : 16
Age : 31
Date d'inscription : 21/03/2009
| | Sujet: Re: toc toc toc! olympiades Dim 22 Mar 2009, 11:19 | |
| jé pas bien compri linégalité, veuillez m'expliquer svp, et merci d'avance! | |
|
| | |
mouad01
Maître
Nombre de messages : 271
Age : 32
Localisation : dans la lune ou sur le nuage qui me transporte
Date d'inscription : 12/04/2008
| | Sujet: Re: toc toc toc! olympiades Dim 22 Mar 2009, 11:27 | |
| jcompren tjr pas dou vient le X merci tt dmeme si une explication plus détaillé et possible..  | |
|
| | |
stil2med
Expert grade2
Nombre de messages : 367
Age : 33
Localisation : oujda
Date d'inscription : 02/11/2008
| | Sujet: Re: toc toc toc! olympiades Dim 22 Mar 2009, 12:11 | |
| x=R2/2 ou x = -R2/2
R c le racine | |
|
| | |
Invité
Invité
| | Sujet: Fraction continue Dim 22 Mar 2009, 12:20 | |
| Bonjour ce sujet m'as interpellé aussitot c'est trés connu comme fraction continue . 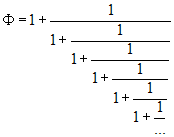 La méthode réside dans le fait que chaque x_1 est la partie entiére X au reste on effectue la même opération.  |
|
| | |
mouad01
Maître
Nombre de messages : 271
Age : 32
Localisation : dans la lune ou sur le nuage qui me transporte
Date d'inscription : 12/04/2008
| | Sujet: Re: toc toc toc! olympiades Dim 22 Mar 2009, 13:07 | |
| ah je vois désolé jsavé pas ksété un cours d'étude supérieur.
en lisant le cours jé compris donc que x qu'on a là et 1<x<2 XD c tout ce que je suis arrivé a faire mais pr la methode pr trouvé la valeur de x jné pa réussi meme en lisant 5 fois le cours dans different site, ya t il une methode facil a suivre???? | |
|
| | |
Invité
Invité
| | Sujet: Re: toc toc toc! olympiades Dim 22 Mar 2009, 13:12 | |
| Ceci n'est pas un cours juste un effort personnel .
Pour comprendre essaye d'écrire pi sous fractions continue aprés tu verras que cela est triviale et trés linéaire.
En réponse à Milor18 la limite d'une fraction continue est bien la valeur du nombre x initial cependant sa fraction elle descend sans fin comme un escalier sans fin qu'on descend l'analogie nous permet de dire que cette fraction ne finit pas.
Bonne chance.
Dernière édition par Moncefelmoumen le Dim 22 Mar 2009, 13:21, édité 2 fois |
|
| | |
mouad01
Maître
Nombre de messages : 271
Age : 32
Localisation : dans la lune ou sur le nuage qui me transporte
Date d'inscription : 12/04/2008
| | Sujet: Re: toc toc toc! olympiades Dim 22 Mar 2009, 13:18 | |
| merci Moncefelmoumen pr les info , et la réponse de milor me parait pausible jcompren mieu merci a tous | |
|
| | |
mouad01
Maître
Nombre de messages : 271
Age : 32
Localisation : dans la lune ou sur le nuage qui me transporte
Date d'inscription : 12/04/2008
| | Sujet: Re: toc toc toc! olympiades Dim 22 Mar 2009, 19:26 | |
| voila c sa Quelles sont les solutions de cette équation ? Expliquez <a href="http://www.casimages.com/img.php?i=090322082440312082.gif" >Cliquez ici pour voir mon image</a> | |
|
| | |
mouad01
Maître
Nombre de messages : 271
Age : 32
Localisation : dans la lune ou sur le nuage qui me transporte
Date d'inscription : 12/04/2008
| | Sujet: Re: toc toc toc! olympiades Dim 22 Mar 2009, 19:29 | |
| arffff pa lresulta attendu mé c bien sa
http://www.casimages.com/img.php?i=090322082440312082.gif
pr ceux ki voulaient comprendre linegalité
a+ | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: toc toc toc! olympiades | |
| |
|
| | |
| | toc toc toc! olympiades | |
|
