olyyyyyyyyyyyyyy

Sujet: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 18:15

بسم الله الرحمن الرحيم

تعتبر تمارين اولمبياد الرياضيات مواضيع غنية بالوضعيات التي تمكن من ادماج التعلمات و تسخير القدرات، نضرا لطابعها الخاص الدي يتطلب نمطا متميزا من التفكير و ابرلز المهارات .
و ليس الهدف الرئيسي من انجاز هده التمارين هو وضع التلميد في محك مع موضوع المعرفة ومع نفسه ، بل هو ايضا الارتقاء بالتلميد الى درجة اعلى من التمكن في استعمال و توضيف معارفه و استتمار قدراته في مواجهة وضعيات المسائل ، ودلك من اجل اكتساب كفايات منهجية و استراتيجية .
فالمتفاوتات مكون رئيسي في تمارين الاولمبياد ، بالطبع الى جانب الهندسة و نضرية الاعداد و الجبر ... و الالمام بقواعد هدا العلم له فوائد عديدة خاصة للمقبلين على مباريات اولمبياد الرياضيات ، ففي المغرب وبالتحديد اولمبياد السنة الاولى و التانية علوم رياضية دائما ما يكون ضمن التمارين الاربعة متفاوتة و لا داعي لتضييع الخمس نقط المترتبة عنها و بالتالي ضمان امل للتأهل للمرحلة المقبلة

متفاوتة Cauchy schwartz

ليكن $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و ...و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و ...و $olyyyyyyyyyyyyyy Mimetex$ اعداد حقيقية موجبة قطعا :

$olyyyyyyyyyyyyyy Mimetex.cgi?(a_1^2+a_2^2+....+a_n^2)(b_1^2+b_2^2+....+b_n^2) \geq \: (a_1b_1+a_2b_2+...$

تطبيقات لمتفاوتة Cauchy schwartz :

مثال اول :

بوضع $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ نجد

$olyyyyyyyyyyyyyy Gif.latex?\120dpi (x_1+x_2+x_3+.....)(\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}+....$

مثال ثاني :

بوضع $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ نجد هده المتفاوتة الجميلة :

$olyyyyyyyyyyyyyy Mimetex$

$olyyyyyyyyyyyyyy Mimetex$

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 18:21

متفاوتة schur :

ليكن $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ اعداد حقيقية موجبة و $olyyyyyyyyyyyyyy Mimetex$ :

$olyyyyyyyyyyyyyy Mimetex$

مع التساوي ادا و فقط ادا كان $olyyyyyyyyyyyyyy Mimetex$ او عددين متساويين و الاخر منعدم .

تطبيقات لمتفاوتة schur :

مثال اول :

باخد $olyyyyyyyyyyyyyy Mimetex$ نجد :

$olyyyyyyyyyyyyyy Mimetex$

مثال ثاني :

باخد $olyyyyyyyyyyyyyy Mimetex$ نجد :

$olyyyyyyyyyyyyyy Mimetex$

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 18:30

متفاوتة jensen

لتكن $olyyyyyyyyyyyyyy Mimetex$ دالة معرفة $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و .....و $olyyyyyyyyyyyyyy Mimetex$ من المجال $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و .....و $olyyyyyyyyyyyyyy Mimetex$ اعداد حقيقية موجبة .

ادا كانت $olyyyyyyyyyyyyyy Mimetex$ دالة محدبة :

$olyyyyyyyyyyyyyy Mimetex.cgi?\omega_1f(x_1)+\omega_2f(x_2)+....+\omega_nf(x_n) \: \geq \: (\omega_1+\omega_2+....+\omega_n)f(\frac{\omega_1x_1+\omega_2x_2+....+\omega_nx_n}{\omega_1+\omega_2+...$

ادا كانت $olyyyyyyyyyyyyyy Mimetex$ دالة مقعرة :

$olyyyyyyyyyyyyyy Mimetex.cgi?\omega_1f(x_1)+\omega_2f(x_2)+....+\omega_nf(x_n) \: \le \: (\omega_1+\omega_2+....+\omega_n)f(\frac{\omega_1x_1+\omega_2x_2+....+\omega_nx_n}{\omega_1+\omega_2+...$

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 18:36

تطبيقات لمتفاوتة jensen

$olyyyyyyyyyyyyyy Gif$

$olyyyyyyyyyyyyyy Gif.latex?\120dpi M$

$olyyyyyyyyyyyyyy Gif$

soulution

olyyyyyyyyyyyyyy Wh_85136719

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 18:42

متفاوتة المثلث

اذا كانت المتغيرات اضلاع مثلت $olyyyyyyyyyyyyyy Mimetex$ فان العلاقة التالية محققة لجميع اضلاع اي مثلت :

$olyyyyyyyyyyyyyy Mimetex$

و يمكن تعويضها بمتغيرات اخرى $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ بحيث :

$olyyyyyyyyyyyyyy Mimetex$

ومع هذا التغيير يمكن ايجاد هذه النتيجة المهمة :

$olyyyyyyyyyyyyyy Mimetex$

اذا تحقق الشرط $olyyyyyyyyyyyyyy Mimetex$ في مثلت زواياه حادة بحيث [img(144,23)]http://www.ballighoemails.com/cgi-bin/mimetex.cgi?\alpha \: ,\: \beta \: ,\: \gamma \: \in \: ]0 \: , \: \frac{\pi}{2}[[/img] فانه يمكن تحويل هده المتغيرات الى متغيرات اخرى تحقق دلك الشرط :

$olyyyyyyyyyyyyyy Mimetex$

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 18:49

تطبيقات لمتفاوتة المثلت :

و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ أضلاع مثلث 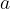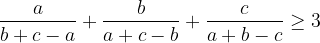$olyyyyyyyyyyyyyy Gif$

$olyyyyyyyyyyyyyy Gif.latex?\120dpi M$

$olyyyyyyyyyyyyyy Gif$

soulution

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 18:52

متفاوتات الوسط : التربيعي -الحسابي -الهندسي -التوافقي

ليكن $olyyyyyyyyyyyyyy Mimetex$ من $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ من $olyyyyyyyyyyyyyy Mimetex$ حيث $olyyyyyyyyyyyyyy Mimetex.cgi?i \in \{1 , 2 , 3 , . .$

$olyyyyyyyyyyyyyy Mimetex$

و يتحقق التساوي ادا و فقط ادا كان : $olyyyyyyyyyyyyyy Mimetex.cgi?x_1=x_2=...$

في حالة عددين حقيقين موجبين تصبح المتفاوتات على الشكل :

$olyyyyyyyyyyyyyy Mimetex$

مع التساوي ادا و فقط ادا كان $olyyyyyyyyyyyyyy Mimetex$

تطبيقات لمتفاوتة الوسط التربيعي-الحسابي-الهندسي-التوافقي

مثال اول

لدينا حسب متفاوتة الوسط الحسابي -الهندسي لثلاتة اعداد :

$olyyyyyyyyyyyyyy Mimetex$

لدينا حسب متفاوتة الوسط التربيعي-الحسابي لثلاتة اعداد :

$olyyyyyyyyyyyyyy Mimetex$

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 18:54

متفاوتة Bernoulli

ليكن $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ عددين حقيقين بحيث : $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$

$olyyyyyyyyyyyyyy Mimetex$

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 18:56

متفاوتة Chebyshev

ليكن $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و .....و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و .....و $olyyyyyyyyyyyyyy Mimetex$ اعداد حقيقية بحيث :

$olyyyyyyyyyyyyyy Mimetex.cgi?{a_1 \le a_2 \le ....$ و $olyyyyyyyyyyyyyy Mimetex.cgi?{b_1 \le b_2 \le ....$

$olyyyyyyyyyyyyyy Mimetex.cgi?\frac{a_1b_1+a_2b_2+...+a_nb_n}{n} \: \geq \: \Bigg(\frac{a_1+a_2+....+a_n}{n}\Bigg)\Bigg(\frac{b_1+b_2+....+b_n}{n}\Bigg) \: \geq \: \frac{a_1b_n+a_2b_{n-1}+...$

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 18:58

weighted AM-GM inequality

ليكن $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و .... و $olyyyyyyyyyyyyyy Mimetex$ اعداد حقيقية موجبة قطعا بحيث : $olyyyyyyyyyyyyyy Mimetex.cgi?\omega_1 +\omega_2+...$

لكل $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و ....و $olyyyyyyyyyyyyyy Mimetex$ اعداد حقيقية موجبة قطعا ، المتفاوتة التالية محققة :

$olyyyyyyyyyyyyyy Mimetex.cgi?\omega_1x_1 +\omega_2x_2+....+\omega_nx_n \: \geq \: x_1^{\omega_1 }x_2^{\omega_2} \:....$

و يتحقق التساوي ادا و فقط اذا كان $olyyyyyyyyyyyyyy Mimetex.cgi?x_1=x_2=...$

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 19:00

متفاوتة Minkowski

ليكن $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و ....و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و ....و $olyyyyyyyyyyyyyy Mimetex$ اعداد حقيقية موجبة قطعا و $olyyyyyyyyyyyyyy Mimetex$

$olyyyyyyyyyyyyyy Mimetex$

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 19:03

متفاوتة Holder

ليكن $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و ....و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و ....و $olyyyyyyyyyyyyyy Mimetex$ اعداد حقيقية موجبة و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ عددين حقيقين موجبين قطعا بحيث : $olyyyyyyyyyyyyyy Mimetex$

$olyyyyyyyyyyyyyy Mimetex.cgi?\huge{\frac{a_1b_1+a_2b_2+....+a_nb_n }{n} \le \bigg(\frac{a_1^p+a_2^p+....+a_n^p}{n}\bigg)^{\frac{1}{p}} \: \bigg(\frac{a_1^q +a_2^q+...$

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 19:04

متفاوتة Huygens

لتكن $olyyyyyyyyyyyyyy Mimetex$ و ....و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و ....و $olyyyyyyyyyyyyyy Mimetex$ و $olyyyyyyyyyyyyyy Mimetex$ و ....و $olyyyyyyyyyyyyyy Mimetex$ اعداد حقيقية موجبة بحيث : $olyyyyyyyyyyyyyy Mimetex.cgi?p_1+p_2+...$

$olyyyyyyyyyyyyyy Mimetex$

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 19:08

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 19:20

merci issam!!! mé fallait mieux les poster ds le forum de theo.

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 19:31

derien mon ami zakaria mais machi mochkil wakha ndirom fl premiere machi mochkil hit l premiere homa li raydwzo olyyyy

Sujet: Re: olyyyyyyyyyyyyyy Mar 17 Nov 2009, 22:28

bonsoir tu peux poster la source ou tu as pris ces théo ?

Sujet: Re: olyyyyyyyyyyyyyy Mer 18 Nov 2009, 15:45

Merci Issam Smile

Sujet: Re: olyyyyyyyyyyyyyy Mer 18 Nov 2009, 21:27

Excusez moi , mais si jamais on fais face à ce genre d'exercices est-ce qu'il suffit de dire d'après l'inégalité de xxx on a : x+y.... ??

Sujet: Re: olyyyyyyyyyyyyyy Jeu 19 Nov 2009, 05:19

bjr ...
Heu oui mais tache de présenter tout les conditions de l'inéquation ^^

Sujet: Re: olyyyyyyyyyyyyyy Jeu 19 Nov 2009, 13:18

Ah d'accord Merci ^^

Sujet: Re: olyyyyyyyyyyyyyy Jeu 19 Nov 2009, 17:01

merci issam

Sujet: Re: olyyyyyyyyyyyyyy Jeu 19 Nov 2009, 17:46

MERCI POUR VOS EFFORTS issam erriahi .

Sujet: Re: olyyyyyyyyyyyyyy Jeu 19 Nov 2009, 19:13

Bonsoir,

Est-t-il vraiment nécessaire de spécifier le nom de l'inégalité?

Et puis merci beaucoup Issam.

Et bonne chance à tous le monde. ALLAH iy3awna jami3an.

Sujet: Re: olyyyyyyyyyyyyyy Jeu 19 Nov 2009, 19:33

Rebonsoir.

Il y a une faute au niveau du message classé N°6 dans la discussion.
Il faut plutôt mettre [(y/2x)+(z/2x)+(x/2y)+(z/2y)+(x/2z)+(y/2z)].