demande d'aide de issam riahi

J'ai trouvé cette solutio dans le forum de première mais elle est proche du tronc commun (de issam erriahi)
soulution de problem

remarque

linobayn anaho ida kana fa ina
=<
=<
[img]http://latex.codecogs.com/gif.latex?2(\frac{2}{1+x^2}+\frac{2}{1+y^2})=4[1+\frac{1-x^2y^2}{(1+x^2)(1+y^2)}][/img]
=< [img]http://latex.codecogs.com/gif.latex?4[1+\frac{1-x^2y^2}{(1+xy)^2}]=\frac{8}{1+xy}=\frac{8}{z+1}[/img]
donc
=<
idan yakfi an nobayn ana
=<
wa bima ana
=<
fa yakfi an nobayn ana
=<
al motafawita al akhira tokafia
>=
tokafiaa
>=
donc

veut pouver corriger les deux ligne .j'arrive pas a le lire
[img]http://latex.codecogs.com/gif.latex?2(\frac{2}{1+x^2}+\frac{2}{1+y^2})=4[1+\frac{1-x^2y^2}{(1+x^2)(1+y^2)}][/img]
=< [img]http://latex.codecogs.com/gif.latex?4[1+\frac{1-x^2y^2}{(1+xy)^2}]=\frac{8}{1+xy}=\frac{8}{z+1}[/img]

et merci d'avance

Voici une solution bien rédigée:

issam erriahi a écrit:

Posons

remarque

linobayn anaho ida kana fa ina
=<
=<
=<
donc
=<
idan yakfi an nobayn ana
=<
wa bima ana
=<
fa yakfi an nobayn ana
=<
al motafawita al akhira tokafia
>=
tokafiaa
>=
donc

Ce qui met fin à cette démonstration.

Au plaisir.

quand il utilise (1+x^2)(1+y^2)>=(1+xy)^2 comment il a montré que 1-(xy)^2>=0

mohamed diai a écrit:

quand il utilise (1+x^2)(1+y^2)>=(1+xy)^2 comment il a montré que 1-(xy)^2>=0

Normalement, il n'a pas montré que est positif.
Cet exercice est l'un des plus durs du programme de tronc commun. Et la démonstration présentée ici est l'une des plus élémentaire que tu puisses trouver.
J'ai cru toujours que l'inégalité est symétrique! Mais il s'est avéré, en lisant dans l'autre topic traitant de cette inégalité, une justification du fait qu'elle ne l'est pas.
Toutefois, on a .
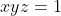
Sans nuire à la généralité du problème, on a le droit de supposer que .
(C'est comme si tu fais une étude de cas: Le premier lorsque les nombres sont égaux, le second lorsqu'ils ne sont pas égaux et là l'un d'eux est supérieur aux deux autres et c'est qui est choisi dans cette démonstration).
Je pense que cela répond à ta question!