En IN:

1/Montrez que le nombre suivant appartient à IN:
.
2/Trouvez n et p tel que:
.
3/Le nombre suivant est-il naturel?
.
Bonne chance.

Pour le deuxième:
On a :

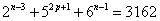
tel que p et n £ IN².
Pour que 2^(n-3) et 6^(n-1) soit des nombres de N on doit avoir: n-3>=0 et n-1>=0.
Donc n>=3.
Si n-3 et n-1 n'égalent pas 0 on a:
2^(n-3) est toujours pair.
5^(2p+1) est toujours impair.
et 6^(n-1) est toujours pair aussi.
Donc 2^(n-1)+5^(2p+1)+6^(n-1)=un nombre impair.
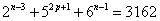
Mais on a et 3162 est pair
Donc soit 2^(n-3) ou 6^(n-1) est impair.
Donc soit n=3 ou n=1.
Et puisque n>=3 on a n=3.
Donc on a: 2^0+5^(2p+1)+6²=3162.
Donc: 1+5^(2p+1)+36=3162.
Donc: 5^(2p+1)+37=3162.
Donc: 5^(2p+1)=3162-37.
Donc: 5^(2p+1)=3125.
Donc: 5^(2p+1)=5^5.
Donc: 2p+1=5.
Donc: 2p=4.
Donc: p=2.
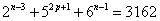
Donc pour que on doit avoir n=3 et p=2.

Les autres exercices sont très faciles car je les ai tiré du manuel de la deuxième année du collège.
Je vous souhaite bonne chance.
Je donne la réponse après.