| | un nouveau test d'ly pour vous |  |
|
+3houssam110 Fermat-X the kiler 7 participants |
|
| Auteur | Message |
|---|
the kiler
Maître
 Nombre de messages : 192 Nombre de messages : 192
Age : 30
Date d'inscription : 18/02/2010
 |  Sujet: un nouveau test d'ly pour vous Sujet: un nouveau test d'ly pour vous  Ven 26 Fév 2010, 12:20 Ven 26 Fév 2010, 12:20 | |
| http://dc153.4shared.com/download/230200071/112882f/New_Document.pdf?tsid=20100226-071817-f05628f3 | |
|
  | |
the kiler
Maître
 Nombre de messages : 192 Nombre de messages : 192
Age : 30
Date d'inscription : 18/02/2010
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Ven 26 Fév 2010, 13:06 Ven 26 Fév 2010, 13:06 | |
| yalah les amis.participez svp | |
|
  | |
Fermat-X
Maître

 Nombre de messages : 99 Nombre de messages : 99
Age : 31
Date d'inscription : 22/11/2008
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Ven 26 Fév 2010, 13:48 Ven 26 Fév 2010, 13:48 | |
| pour le 2 éme ex il faut que k et n et m soit different de 1 !! | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Ven 26 Fév 2010, 14:02 Ven 26 Fév 2010, 14:02 | |
| salam
2eme Exo:
si m=n=k=0 on aura f(0)=1 ==> car -(f(0)-1)²>=0
si m=n=k=1 on aura f(1)=1==> car -(f(1)-1)²>=0
si k=0 et m=1
on aura
f(n)=<1
sin m=n=1
on aura f(k)>=1
donc f(n)=1 pour tt n de IN | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Ven 26 Fév 2010, 14:55 Ven 26 Fév 2010, 14:55 | |
| oué absolument houssam...
Dernière édition par majdouline le Ven 26 Fév 2010, 15:05, édité 1 fois | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Ven 26 Fév 2010, 15:01 Ven 26 Fév 2010, 15:01 | |
| C'est plutôt 1+1-1>=1
Donc la fonction f(n)=1 vérifie bien les conditions .. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Ven 26 Fév 2010, 15:48 Ven 26 Fév 2010, 15:48 | |
| Exercice2:que je trouve trivial..... j'ai trouvé la meme solution que celle de houssam.... on a donc f(1)=1 et f(0)=1....alors m=n=0 on a (∀k∈IN) 1≥f(k) (1) pour m=n=1 on aura : (∀k∈IN) :f(k)≥1(2) de (1) et (2) on a donc : (∀k∈IN) :f(k)=1 Exercice 3:posons x=tan(a) et y=tan(b) et z=tan(c) tel que a,b et c sont les angles d'un triangle et que:  ==>a+b+c=pi la condition x+y+z=xyz est bien vérifiée car tan(a)+tan(b)+tan(c)=tan(a).tan(b).tan(c) on a donc:  et :  ainsi l'inégalité est équivalente à:  ce qui est clairement vrai...... avec égalité si et seulement si: 
Dernière édition par majdouline le Ven 26 Fév 2010, 16:02, édité 1 fois | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Ven 26 Fév 2010, 15:54 Ven 26 Fév 2010, 15:54 | |
| je vien de trouver la meme majdouline pour le 3eme Exo c sa!! | |
|
  | |
the kiler
Maître
 Nombre de messages : 192 Nombre de messages : 192
Age : 30
Date d'inscription : 18/02/2010
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Ven 26 Fév 2010, 16:19 Ven 26 Fév 2010, 16:19 | |
| | |
|
  | |
the kiler
Maître
 Nombre de messages : 192 Nombre de messages : 192
Age : 30
Date d'inscription : 18/02/2010
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Ven 26 Fév 2010, 21:28 Ven 26 Fév 2010, 21:28 | |
| yallah les amis.est ce que vous etes fatigués ou qoi.oh???? | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Ven 26 Fév 2010, 22:52 Ven 26 Fév 2010, 22:52 | |
| | |
|
  | |
the kiler
Maître
 Nombre de messages : 192 Nombre de messages : 192
Age : 30
Date d'inscription : 18/02/2010
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Sam 27 Fév 2010, 01:18 Sam 27 Fév 2010, 01:18 | |
| demain je vais poster les solutions | |
|
  | |
the kiler
Maître
 Nombre de messages : 192 Nombre de messages : 192
Age : 30
Date d'inscription : 18/02/2010
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Sam 27 Fév 2010, 12:42 Sam 27 Fév 2010, 12:42 | |
| si (x,y,z,t) est un solution de probleme .les quadruples (yzt-x,y,z,t),(x,xzt-y,z,t),(x,y,xyt-z,t) et (x,y,z,xyz-t) l'est aussi
on a aussi le quadruple (1,2,3,4) est un solution
...............est on va trouver des solutions plus grande | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Sam 27 Fév 2010, 13:27 Sam 27 Fév 2010, 13:27 | |
| | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Sam 27 Fév 2010, 13:37 Sam 27 Fév 2010, 13:37 | |
| TRes jolie la solution du 1er Exo...
pour corriger c po l'olympiade 2004 de 1er SM mais plutot de la 1er année CPGE et aussi bac SM..
Dernière édition par houssam110 le Sam 27 Fév 2010, 20:56, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 | |
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Sam 27 Fév 2010, 16:41 Sam 27 Fév 2010, 16:41 | |
|
Dernière édition par houssam110 le Sam 27 Fév 2010, 20:58, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Sam 27 Fév 2010, 20:30 Sam 27 Fév 2010, 20:30 | |
| \geq&space;0) implique \leq&space;1) , pas \geq&space;1) . Ce qui finalement ne fait pas vraiment évoluer les choses. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Mar 02 Mar 2010, 14:04 Mar 02 Mar 2010, 14:04 | |
| | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Mar 02 Mar 2010, 21:09 Mar 02 Mar 2010, 21:09 | |
| bonsoir dijkschneier
je crois que c pas possible de le calculer
car on aura
f(km)+f(kn)>=1+f(k)f(mn)
or on aura ici toujour f(k) majorée par 1 et si on réussi a minorer f(km) on va négliger les nombres premiers car on a po le droit de remplacer n ou m par 1 ... or koikon fait on aura jamé une réponse complete a f:E--> IR tel que
c cke je pense
si vs avé une réponse postez la
A+ | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Mar 02 Mar 2010, 21:21 Mar 02 Mar 2010, 21:21 | |
| - houssam110 a écrit:
car on aura
f(km)+f(kn)>=1+f(k)f(mn)
or on aura ici toujour f(k) majorée par 1 et si on réussi a minorer f(km) on va négliger les nombres premiers car on a po le droit de remplacer n ou m par 1 ... Je n'ai pas très bien compris ton analyse. Merci de clarifier tout cela. Je vous assure de mon côté qu'il est possible de retrouver la fonction. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Mer 03 Mar 2010, 20:22 Mer 03 Mar 2010, 20:22 | |
| - Citation :
- Soit E l'ensemble
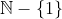 . .
Trouvez toutes les fonctions 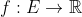 telles que : telles que :
\in%20E^3%20\;%20\;%20\;%20f(km)+f(kn)-f(k)f(mn)%20\geq%201) Solution :Il est facile de prouver que =1) et que \leq%201) pour tout k de E. (0) Posant m=0, il vient que : +f(kn)-(k)f(0)%20\geq%201%20\Leftrightarrow%20f(kn)\geq%20f(k)) , pour tout k et n de E. (1) Posant k=m, il vient que : +f(mn)-f(m)f(mn)\geq%201%20\Leftrightarrow%20f(mn)(1-f(m))+f(m^2)\geq%201%20\Leftrightarrow%20f(mn)(1-f(m))\geq%200%20\Leftrightarrow%20f(mn)\geq%200%20\Leftrightarrow%20f(a)\geq%200) , pour tout a de E. (2) ----------------- Revenons maintenant à l'inéquation initiale : +f(kn)-f(k)f(mn)\geq%201) D'après la seconde propriété, l'on a f(mn)\geq%200%20\Leftrightarrow%20-f(k)f(mn)\leq%200) . L'inéquation devient : +f(kn)\geq%201) Or, \geq%20f(km)) et \geq%20f(kn)) d'après la première propriété. D'où : \geq%201%20\Leftrightarrow%20f(a)\geq%20\frac{1}{2}) pour tout a de E. (3) Revenons encore une fois à l'inéquation de départ : +f(kn)-f(k)f(mn)\geq%201) D'après la troisième propriété, l'on a f(mn)\geq%20\frac{1}{4}%20\Leftrightarrow%20-f(k)f(mn)\leq%20-\frac{1}{4}) L'inéquation devient : \geq%20\frac{1}{4}+1%20=%20\frac{5}{4}%20\Leftrightarrow%20f(a)\geq%20\frac{5}{8}) , pour tout a de E. ---------------- On peut répéter ce processus autant de fois qu'on veut, et à chaque fois, on trouve une meilleur minoration à la fonction. A l'infini, cela tend vers 1 : \geq%201) , pour tout a de E. Et puisque (0), on conclut que =1) , pour tout a de E. Inversement, la fonction h =1) satisfait les conditions de l'énoncé. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Mer 03 Mar 2010, 20:36 Mer 03 Mar 2010, 20:36 | |
| - Dijkschneier a écrit:
-
- Citation :
- Soit E l'ensemble
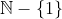 . .
Trouvez toutes les fonctions 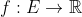 telles que : telles que :
\in%20E^3%20\;%20\;%20\;%20f(km)+f(kn)-f(k)f(mn)%20\geq%201) Solution :
Il est facile de prouver que =1) et que et que \leq%201) pour tout k de E. (0) pour tout k de E. (0)
Posant m=0, il vient que :
+f(kn)-(k)f(0)%20\geq%201%20\Leftrightarrow%20f(kn)\geq%20f(k)) , pour tout k et n de E. (1) , pour tout k et n de E. (1)
Posant k=m, il vient que :
+f(mn)-f(m)f(mn)\geq%201%20\Leftrightarrow%20f(mn)(1-f(m))+f(m^2)\geq%201%20\Leftrightarrow%20f(mn)(1-f(m))\geq%200%20\Leftrightarrow%20f(mn)\geq%200%20\Leftrightarrow%20f(a)\geq%200) , pour tout a de E. (2) , pour tout a de E. (2)
-----------------
Revenons maintenant à l'inéquation initiale :
+f(kn)-f(k)f(mn)\geq%201)
D'après la seconde propriété, l'on a f(mn)\geq%200%20\Leftrightarrow%20-f(k)f(mn)\leq%200) . .
L'inéquation devient : +f(kn)\geq%201)
Or, \geq%20f(km)) et et \geq%20f(kn)) d'après la première propriété. d'après la première propriété.
D'où : \geq%201%20\Leftrightarrow%20f(a)\geq%20\frac{1}{2}) pour tout a de E. (3) pour tout a de E. (3)
Revenons encore une fois à l'inéquation de départ :
+f(kn)-f(k)f(mn)\geq%201)
D'après la troisième propriété, l'on a f(mn)\geq%20\frac{1}{4}%20\Leftrightarrow%20-f(k)f(mn)\leq%20-\frac{1}{4})
L'inéquation devient : \geq%20\frac{1}{4}+1%20=%20\frac{5}{4}%20\Leftrightarrow%20f(a)\geq%20\frac{5}{8}) , pour tout a de E. , pour tout a de E.
----------------
On peut répéter ce processus autant de fois qu'on veut, et à chaque fois, on trouve une meilleur minoration à la fonction.
A l'infini, cela tend vers 1 : \geq%201) , pour tout a de E. , pour tout a de E.
Et puisque (0), on conclut que =1) , pour tout a de E. , pour tout a de E.
Inversement, la fonction h=1) satisfait les conditions de l'énoncé. satisfait les conditions de l'énoncé. bonsoir.... oué ...et alors c'est exactement ce que j'ai cru  ... regarde ta quatrième ligne ce n'est pas pour tout a de E mais plutot pour tout a non premier.... encore dans la (3) c'est pas pour a de E mais plutot pour tout a ayant trois (ou plus) de diviseurs.... et à la fin en repetant ce processus étant de fois qu'on veut...ça sera pas vrai pour tout a de E mais plutot pour tout a ayant une infinité de diviseurs.... ton raisonnement est donc faux..... | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Mer 03 Mar 2010, 20:45 Mer 03 Mar 2010, 20:45 | |
| Absolument Majdouline c cke je luié dit dans mon dernier message ... (je sé ke je me sius exprimé mal)^^ | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  Jeu 04 Mar 2010, 11:51 Jeu 04 Mar 2010, 11:51 | |
| Tout à fait. Pardon de vous avoir importuner avec un "problème" contrefait. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: un nouveau test d'ly pour vous Sujet: Re: un nouveau test d'ly pour vous  | |
| |
|
  | |
| | un nouveau test d'ly pour vous |  |
|
