defie géometrie - triangle !!!!

soit un triangle ABC dont les angles ne depassant pas 2pi/3.
trouvez l'emplacement d'un point M tel que la somme MA+MB+MC soit minimale!!!!!!!!!!!!!!!!!!

M = G du triangle ?

firedow a écrit:

soit un triangle ABC dont les angles ne depassant pas 2pi/3.
trouvez l'emplacement d'un point M tel que la somme MA+MB+MC soit minimale!!!!!!!!!!!!!!!!!!

BJR firedow !!!

J'ai vu cet exo posé d'une part sur le Forum ici et sur l'autre Forum Mathsland .... il a été posé par lilo_khalou
Alors serais-tu lilo_khalou ??? Pas Grave ....

On me reproche à tort ou à raison de fourrer mon nez partout .... Je ne crois pas ...
Je réponds à qui je veux et je réponds parfois lorsque personne ne veut intervenir ... Je réponds aussi lorsque j'y trouve du FUN !!!

Pour ton exo :

1) Remarquer que rendre Minimale la Somme des longueurs MA+MB+MC c'est pareil que rendre Minimale MA^2+MB^2+MC^2

il s'agit là de la somme des Carrés des Distances !!

2) Tu pourrais alors faire intervenir un point particulier G qui s'appelle le Centre de Gravité du Triangle ABC .
Ce point a la particularité de vérifier GA+GB+GC=0 ( en Vecteurs ) .
Tu écriras alors MA^2=(MG+GA)^2=MG^2+GA^2+2.<MG,GA>
expression dans laquelle <MG,GA> désigne le Produit Scalaire des Vecteurs MG et GA .
Ecrite aussi pour les points B et C , tu obtiendras par Sommation :
MA^2+MB^2+MC^2=3.MG^2 + {GA^2+GB^2+BC^2} + 2.<MG;GA+GB+GC>
et puisque GA+GB+GC=0 ( en Vecteurs ) :
MA^2+MB^2+MC^2=3.MG^2 + {GA^2+GB^2+BC^2}

3) Il est facile de voir que cette expression , dépendant du point M , est Minimale lorsque
MG=0 donc M=G , Centre de Gravité du triangle ABC .

LHASSANE

PS : @ M.Marjani , c'est donc exact et tu en as une démonstration ci-jointe ....

c'est moi lilo_khalou xD merci pour la reponse

firedow a écrit:

soit un triangle ABC dont les angles ne depassant pas 2pi/3.
trouvez ....

La réponse est bien M=G
Par contre , je ne vois pas pourquoi cette condition restrictive ..... Peu importe même si le triangle ABC est obtuangle , son Centre de Gravité se trouve toujours en son intérieur ......
C'est l'Orthocentre , point de Concours des trois Hauteurs qui peut se trouver en dehors du triangle ....

LHASSANE

Citation :

3) Il est facile de voir que cette expression , dépendant du point M , est Minimale lorsque
MG=0 donc M=G , Centre de Gravité du triangle ABC

Jai pas bien compris cette etape merci de expliquer plus

BSR lilo_khalou !!

On a montré que pour tout point du plan :
MA^2+MB^2+MC^2=3.MG^2 + {GA^2+GB^2+BC^2}

Donc MA^2+MB^2+MC^2 >= GA^2+GB^2+BC^2
puisque 3.MG^2 est toujours positif .
Introduisons la fonction Ponctuelle f suivante :
f : M ------> f(M)=MA^2+MB^2+MC^2

On a f(M) >= f(G) pour tout point M
Donc f(G) est la valeur Minimale de f(M) lorsque M décrit le plan usuel
et ce Minimum Absolu est atteint lorsque M=G .

LHASSANE

Bonsoir

ce point est appelé point de Fermat, il coincide avec le centre de gravité dans un seul cas, dans le cas du triangle équilatéral

il y a deux de méhodes pour répondre à cette question- la première utilise la rotation de centre l'un des sommets de ce triangle et d'angle de 60° ou -60° selon l'orientation du triangle. la deuxième utilise simplement le théorème d'alkhachi

BSR ABB !!

J'ai été voir sur la Toile .... En effet , il s'agit bien de ce que tu appelles le Point de FERMAT !!
Drôlement alambiquée comme construction ....
Celà étant , ou se trouve l'erreur sournoise dans ma démarche ??
Sans doute ceci :
Le point M qui MINIMISE l'application
U ---------> f(U)=||UA|| + ||UB|| + ||UC||

n'est pas toujours celui N qui MINIMISE l'application
V ----------> g(V)=||VA||^2 + ||VB||^2 + ||VC||^2

C'est celà .....
Merci bcp pour ta réactivité car je ne connaissais franchement pas !!! LHASSANE

Oeil_de_Lynx a écrit:

BSR ABB !!
Sans doute ceci :
Le point M qui MINIMISE l'application
U ---------> f(U)=||UA|| + ||UB|| + ||UC||

n'est pas toujours celui N qui MINIMISE l'application
V ----------> g(V)=||VA||^2 + ||VB||^2 + ||VC||^2

C'est celà .....

L'on a d'après CS, donc, si A est le minimum de f, le minimum de g est 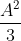. Ces minimums sont clairement différents.

j'ai aussi fait des recherche sur ce POINT de FERMAT mais j'ai pa trouver de démonstration !!
Qui peut m'aider à en trouver ?!