Un système:

Résolvez en $Un système: Gif$ ce système:
$Un système: Gif$ .
Sachant que a est un réel positif.
Bonne chance.

Dernière édition par mizmaz le Jeu 28 Oct 2010, 20:06, édité 1 fois

nmo a écrit:: Résolvez en $Un système: Gif$ ce système:
$Un système: Gif$ .
Sachant que a est un réel positif.
Bonne chance.

Par un simple raisonnement par disjonction des cas, il est aisé d'établir l'équivalence suivante :
$Un système: Gif$
Il suffit, en effet de considérer les trois cas suivants :
$Un système: Gif$ , $Un système: Gif$ et $Un système: Gif$
Appelons cette équivalence (1).

Notre système peut être réduit à deux lignes :
$Un système: Gif.latex?\left\{\begin{matrix}%20x_{i}\begin{vmatrix}%20x_{i}%20\end{vmatrix}-(x_{i}-a)\begin{vmatrix}%20x_{i}-a%20\end{vmatrix}=x_{i+1}\begin{vmatrix}%20x_{i+1}%20\end{vmatrix}\\%20x_{n}\begin{vmatrix}%20x_{n}%20\end{vmatrix}-(x_{n}-a)\begin{vmatrix}%20x_{n}-a%20\end{vmatrix}=x_{1}\begin{vmatrix}%20x_{1}%20\end{vmatrix}%20\end{matrix}\right.%20\setminus%20i\in%20\begin{Bmatrix}%201,2,3,4,...,n-1%20\end{Bmatrix}%20\\\Leftrightarrow%20\left\{\begin{matrix}%20x_{i}\begin{vmatrix}%20x_{i}%20\end{vmatrix}-x_{i+1}\begin{vmatrix}%20x_{i+1}%20\end{vmatrix}=(x_{i}-a)\begin{vmatrix}%20x_{i}-a%20\end{vmatrix}%20\\%20x_{n}\begin{vmatrix}%20x_{n}%20\end{vmatrix}-(x_{n}-a)\begin{vmatrix}%20x_{n}-a%20\end{vmatrix}=x_{1}\begin{vmatrix}%20x_{1}%20\end{vmatrix}%20\end{matrix}\right.%20\setminus%20i\in%20\begin{Bmatrix}%201,2,3,4,..$
Intéressons nous à la première ligne :
$Un système: Gif$
Nous avons (En tenant compte de (1)) :
$Un système: Gif$
De cette dernière équivalence, je pense qu'il est possible d'affirmer que :
$Un système: Gif.latex?\forall%20i\in%20\begin{Bmatrix}%201,2,3,4,...,n-1%20\end{Bmatrix}\;%20\setminus%20\;%20x_{i+1}=a%20\\%20\Leftrightarrow%20\forall%20k\in%20\begin{Bmatrix}%202,3,4,5,..$
( $Un système: Gif$ )
Il suffit maintenant de traiter le cas de $Un système: Gif$ à part.
Prenons la dernière ligne du système pour cela :
$Un système: Gif$
Et donc l'ensemble des solutions au système est :
$Un système: Gif.latex?\\%20S=\begin{Bmatrix}%20n\;%20fois\\(\overbrace{a,a,a,a,..$
Sauf erreur, non mais sur ce coup-là, je ne suis vraiment pas sûr de ma démonstration.
Au plaisir ! Smile

Expert sup Nombre de messages : 1482 Age : 30 Date d'inscription : 12/12/2009

Bon exercice, évidemment.
En sommant membre à membre les égalités du système, on obtient $Un système: Gif$
Il convient de remarquer que si, pour un i allant de 1 à n, on a $Un système: Gif$ ou $Un système: Gif$ , alors on déduit systématiquement que $Un système: Gif$ (1)
Supposons que $Un système: Gif$ , et que pour tout i allant de 2 à n, $Un système: Gif$
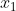
La première égalité du système se traduit alors en $Un système: Gif$ . Mais puisque $Un système: Gif$ , il vient que $Un système: Gif$
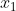
Si $Un système: Gif$ est positif, alors on remarque que $Un système: Gif$ . Mais puisque $Un système: Gif$ , $Un système: Gif$ est négatif. Contradiction. $Un système: Gif$ est donc négatif.
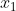
Partons maintenant à la dernière égalité du système $Un système: Gif$
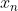
$Un système: Gif$ étant négatif, on peut réécrire $Un système: Gif$ . Ainsi $Un système: Gif$ , d'où $Un système: Gif$ est négatif.
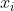
En remontant ainsi dans le système, on finit par prouver que pour tout i allant de 1 à n, $Un système: Gif$ est négatif.
Ainsi, d'après (1), on a dans tous les cas $Un système: Gif$