| | arithmétique !! |  |
|
|
| Auteur | Message |
|---|
yassineno
Maître
 Nombre de messages : 212 Nombre de messages : 212
Age : 31
Localisation : oujda
Date d'inscription : 17/07/2008
 |  Sujet: arithmétique !! Sujet: arithmétique !!  Lun 24 Mai 2010, 00:05 Lun 24 Mai 2010, 00:05 | |
| Soit n un entier naturel.
Montrer que 30 | n^5 - n | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  Lun 24 Mai 2010, 12:09 Lun 24 Mai 2010, 12:09 | |
| n£|N >1 plutot.
------------------------------------------------------------
n^5 - n = n (n^4 - 1) = n (n^2 - 1) (n^2 + 1) = n (n - 1) (n + 1) (n^2 + 1)
D'une autre part: n5 - n = (n – 2) (n – 1) n (n + 1) (n + 2) + 5 (n – 1) n (n + 1)
Remarquons que: 30=5*2*3*1 [produit de 5 et de trois nombres consécutifs; il est divisible par 6 et par le facteur 5 du produit.].
et : 1 x 2 x 3 x 4 x 5 = 120 [produit de cinq nombres consécutifs. Il est divisible par 120].
On a: 120 | (n – 2) (n – 1) n (n + 1) (n + 2)
Et: 30 | 5 (n – 1) n (n + 1)
On sait que: PGCD(120,30) = 30
D'ou: 30 | (n5 – n)
CQFD. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  Jeu 27 Mai 2010, 18:22 Jeu 27 Mai 2010, 18:22 | |
| | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  Jeu 27 Mai 2010, 20:59 Jeu 27 Mai 2010, 20:59 | |
| salam
5 premier ===> fermat : n^5 - n divisible par 5
n^5 - n = (n-1).n.(n+1)....... contient un produit de 3 entiers consécutifs =====> divisible par 6
5 et 6 premiers entre eux ====> n^5 - n divisible par 6.5=30
. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  Ven 28 Mai 2010, 09:56 Ven 28 Mai 2010, 09:56 | |
| - yassineno a écrit:
- Soit n un entier naturel.
Montrer que 30 | n^5 - n Posons  et procédons par récurrence. Pour n=0. On a 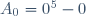 . Donc  . Donc 30 divise 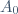 . Supposons que  est divisible par 30 et montrons que  l'est aussi. Pour cela, posons:  . On a ^5-(n+1)) . Donc 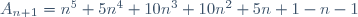 . Donc 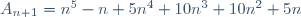 . Donc  . Donc ) . Donc (n^2-n+1)+2n(n+1))) . Donc (n^2-n+1+2n)) . Donc (n^2+n+1)) . On a (n^2+n+1)) est divisible par 6 quelquesoit n. Posons: (n^2+n+1)=6k') . Ainsi,  . Donc  . Donc ) . Avec 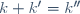 , on obtient  . Il vient que 30 divise  . On conclut que pour tout n de 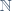 30 divise 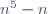 . CQFD. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  Ven 28 Mai 2010, 10:25 Ven 28 Mai 2010, 10:25 | |
| Je termine ce que je viens de commencer: Montrons que 6 divise (n^2+n+1)) quelquesoit n de 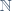 . Posons (n^2+n+1)) et procédons par disjonction de cas: Comme n est un entier, il s'écrit en utilisant l'une de ces expressions:  ou  ou  ou  ou  ou  . Le premier cas:  . On a ((6k)^2+6k+1)) . Donc (36k^2+6k+1)\big)) . Ainsi 6 divise 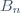 dans ce cas. Le second cas:  . On a (6k+1+1)((6k+1)^2+6k+1+1)) . Donc (6k+2)(36k^2+12k+1+6k+1+1)) . Donc *2*(3k+1)(36k^2+18k+3)) . Donc *2*(3k+1)*3*(13k^2+6k+1)) . Donc (3k+1)(13k^2+6k+1)\big)) . Ainsi 6 divise 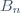 dans ce cas. Le troisième cas:  . On a (6k+2+1)((6k+2)^2+6k+2+1)) . Donc (6k+3)(36k^2+24k+4+6k+2+1)) . Donc *3*(2k+1)(36k^2+30k+7)) . Donc (2k+1)(36k^2+30k+7)\big)) . Ainsi 6 divise 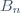 dans ce cas. Le quatrième cas:  . On a (6k+3+1)((6k+3)^2+6k+3+1)) . Donc (6k+4)(36k^2+36k+9+6k+3+1)) . Donc *2*(3k+2)(36k^2+42k+13)) . Donc (3k+2)(36k^2+42k+13)\big)) . Ainsi 6 divise 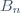 dans ce cas. Le quatrième cas:  . On a (6k+4+1)((6k+4)^2+6k+4+1)) . Donc (6k+5)(36k^2+48k+16+6k+4+1)) . Donc (6k+5)(36k^2+54k+21)) . Donc (6k+5)*3*(13k^2+18k+7)) . Donc (6k+5)(13k^2+18k+7)\big)) . Ainsi 6 divise 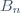 dans ce cas. Le dernier cas:  . On a (6k+5+1)((6k+5)^2+6k+5+1)) . Donc (6k+6)(36k^2+60k+25+6k+5+1)) . Donc *6*(k+1)(36k^2+66k+31)) . Donc (k+1)(36k^2+66k+31)\big)) . Ainsi 6 divise 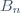 dans ce cas. On conclut que 6 divise (n^2+n+1)) quelquesoit n de 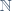 . CQFD. P.S: on pourra faire une longue disjonction de cas pour le problème initiale en posant n=30k ou n=30k+1 jusqu'à n=30k+29. Cela est très fatiguant! Cependant, elle reste l'une des methodes.
Dernière édition par nmo le Ven 28 Mai 2010, 10:38, édité 1 fois | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  Ven 28 Mai 2010, 10:27 Ven 28 Mai 2010, 10:27 | |
| Ceci est un probleme classique de terminale ; il suffit de decomposer 30 en facteur premier entre eux et utiliser le theoreme de Fermat! | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  Ven 28 Mai 2010, 15:26 Ven 28 Mai 2010, 15:26 | |
| Il y'a une généralité qu'il faut savoir et qu'il est utile de démontrer :
Montrer que tout produit de n nombres consécutifs est divisible par n! (factorielle de n) | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  Ven 28 Mai 2010, 16:48 Ven 28 Mai 2010, 16:48 | |
| Ce petit theoreme va-t-il nous etre utile pour cet exercice ? ou bien vous parler en general ...?
Faut-il vraiment le démontrer ? Il parait assez évident car dans Z/nZ il n'ya que n classes d'ou le résultat ! | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  Ven 28 Mai 2010, 17:44 Ven 28 Mai 2010, 17:44 | |
| Considérer le produit de n entiers consécutifs : 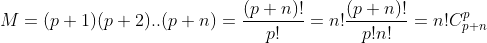 Le résultat en découle .. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  Sam 29 Mai 2010, 10:54 Sam 29 Mai 2010, 10:54 | |
| Soit le produit de n nombres consécutifs commençant par un nombre quelconque t+1
(t+1)(t+2)…(t+n)
= t! (t+1)(t+2)…(t+n) / t!
= 1x2x3 … t*(t+1)(t+2)…(t+n) / t!
= (t+n) ! / t!
= t! (t+n) ! / (t! n!)
= n! Cnt+n
Soit la formule
(t+1)(t+2)…(t+n) = p! Cnt+n
Cnt+n = (t+1)(t+2)…(t+n) / n
Or les coefficients du binôme sont des nombres entiers:
Donc: (t+1)(t+2)…(t+n) est divisible par n!
[Enfin, j'ai étudier un cours (http://fr.wikipedia.org/wiki/Coefficient_binomial) grace à Newton.]
CQFD. | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  Sam 29 Mai 2010, 12:37 Sam 29 Mai 2010, 12:37 | |
| Il y'a des tonnes d'exercices de ce genre qui se cachent dans tout le programme TSM, elle peut aussi être utile au national, c'est une astuce à connaître en somme, mais une astuce parmi tant d'autres. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  Sam 29 Mai 2010, 20:21 Sam 29 Mai 2010, 20:21 | |
| Merci Oussama pour la premiére astuce, je pense que je serais heureux d'honorer le programe SM l'année prochaine au 1bac  | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  Dim 30 Mai 2010, 12:56 Dim 30 Mai 2010, 12:56 | |
| - Othmaann a écrit:
- Ce petit theoreme va-t-il nous etre utile pour cet exercice ? ou bien vous parler en general ...?
(n+1)(n^2+1)) n(n+1)(n+1) est divisible par 3! = 6 Et avec Fermat, on trouve 5/n^5-n D'où la conclusion, mais je dois dire que ce n'est pas le meilleur exercice pour appliquer cette astuce. | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  Dim 30 Mai 2010, 21:40 Dim 30 Mai 2010, 21:40 | |
| salam
c'est bien ma réponse oussama
je ne sais pas pourquoi , cette discussion allongée et inutile.
. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: arithmétique !! Sujet: Re: arithmétique !!  | |
| |
|
  | |
| | arithmétique !! |  |
|
