Orthogonalité belge

EXO:

ABC triangle inscrit dans un cercle de centre O.

On suppose que H le pied de la hauteur issue de A est sur [BC].

le cercle de diamètre [AH] recoupe[AB] en D et [AC] en E.

Montrer que : (OA) est perpendiculaire à (DE) ?

.........................................................................

Soit F l'intersection de (AO) et de (ED).
Soit le triangle AEF. Pour montrer qu'il est rectangle en F, on montre de manière équivalente que .
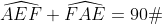
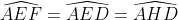
, la dernière égalité étant assurée par le théorème de l'angle inscrit.

(1) : le triangle AOC est isocèle en O.
(2) : théorème de l'angle inscrit.
(3) : le triangle AHB est rectangle en H.

D est un point faisant partie du petit cercle de diamètre [AH], donc le triangle AHD est rectangle en D. Dès lors :
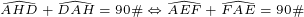
CQFD.

Bonjour Mr Houssam ;
Je vous remercie pour cette series d'EX de geométrie.

Je prends la figure de Dijksheiner et je mensionne sur la figure:



On a crée la droite paralléle à (ED) et passant par H. On l'a appelé (HM). Et: (HM) coup le cercle dont le centre I en T.

D’après la propriété : Si un triangle est inscrit dans un cercle et a pour côté un diamètre de ce cercle, alors cetriangle est rectangle et ce diamètre est l’hypoténuse du triangle, Donc: ATH=90°.
(AO)_|_(HM) donc: (AO)_|_(ED).

Merci.

Joli ! Mais il vous reste à prouver que A, T et O sont colinéaires.

salam

On a : (AO) recoupe le cercle (ABC) en G. ===> [AG] diamètre.

(ED) et (AO) se coupent en K.

DAH + AHD = 90°

DAH = 90° - C = 90°- AGB= BAG
--------------------------------------------
AED = AHD (angles dans le cercle de diamètre [AH])
---------------------------------------------

===>BAG + AED = 90° ( deux angles dans AEK )

conclusion : AKE = 90°

.