|
| | Calcul d'angle encore |  |
| | | Auteur | Message |
|---|
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Calcul d'angle encore Sujet: Calcul d'angle encore  Ven 11 Juin 2010, 06:16 Ven 11 Juin 2010, 06:16 | |
| exo:
ABC un triangle.
La bissectrice intérieure de BAC coupe [BC] en E.
=================== ACB ====[AB] en D
on suppose AD + CE = AC .
trouver l'angle B.
.............................
Dernière édition par houssa le Ven 11 Juin 2010, 22:41, édité 1 fois | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Calcul d'angle encore Sujet: Re: Calcul d'angle encore  Ven 11 Juin 2010, 12:08 Ven 11 Juin 2010, 12:08 | |
| - houssa a écrit:
- exo:
ABC un triangle.
La bissectrice intérieure de BAC coupe [BC] en E.
=================== ACB ====]AC] en D
on suppose AD + CE = AC .
trouver l'angle B.
............................. Je pense que c'est [AB]. Je vais essayer plus tard. | |
|   | | houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: Calcul d'angle encore Sujet: Re: Calcul d'angle encore  Ven 11 Juin 2010, 22:42 Ven 11 Juin 2010, 22:42 | |
| oui c'est bien une erreur : c'est rectifié [AB]
. | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Calcul d'angle encore Sujet: Re: Calcul d'angle encore  Sam 12 Juin 2010, 13:44 Sam 12 Juin 2010, 13:44 | |
| Laissons l'exercice à part quelque temps:
Soit ABC un triangle et soit O le point d'intersection des bissectrices intérieures (le centre de son cercle inscrit).
Soit M, N, et P les projetés orthogonals de O sur (BC), (AC), et (AB).
Posons OM=ON=OP=r.
On a le triangle OMC rectangle en M.
Donc, selon le théorème de pytagore OM²+MC²=OC².
Donc r²+MC²=OC².
De même r²+NC²=OC².
D'où on déduit que r²+MC²=r²+NC².
Donc MC²=NC².
Donc MC=NC.==>(1)
De la même manière, on prouve que AP=AN.==>(2)
De 1 et 2, on trouve que AN+NC=AP+MC.
Donc AC=AP+MC.
Revenons à notre exercice:
On a supposé que AD+CE=AC.
En utilisant ce que je viens de démontrer,
On trouve que E et D sont les projetés respectifs de O sur (AB) et (BC).
(Je ne suis pas sur qu'à 90 pour cent de ce que j'ai dit -en dessinant plusieurs figures, j'ai remarqué que la distance entre le point d'intersection de la bissectrice et le projeté orthogonal sur [BC] ne peut pas être la même sur [AB] que s'ils sont le même point-).
Notons O le point d'intersection de (CD) et (AE).
Posons ECO=c et OAC=a. (angles)
On trouve directement que BAC=2a et ACB=2c. (angles)
La somme des mesures des angles d'un triangle vaut 180°.
Donc ABC+ACB+BAC=180°. (angles)
Donc ABC+2c+2a=180°. (angles)
Donc ABC+2(c+a)=180°. (angles)
Donc ABC=180°-2(c+a).==>(3) (angles)
On a le triangle DAC rectangle en D.
Donc DAC+ACD=90°. (angles)
Donc 2a+c=90°.==>(4) (angles)
De même, on aboutit à 2c+a=90°.==>(5) (angles)
En sommant 4 et 5, on trouve que 2a+c+2c+a=90°+90°. (angles)
Donc 3(a+c)=180°. (angles)
Donc a+c=60°. (angles)
En remplaçant dans 3, on trouve ABC=180°-2*60°.
Donc ABC=180°-120°. (angle)
Donc ABC=60°. (angle)
Bien entendu, j'attends vos remarque. | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Calcul d'angle encore Sujet: Re: Calcul d'angle encore  Sam 12 Juin 2010, 15:06 Sam 12 Juin 2010, 15:06 | |
| - nmo a écrit:
- Laissons l'exercice à part quelque temps:
Soit ABC un triangle et soit O le point d'intersection des bissectrices intérieures (le centre de son cercle inscrit).
Soit M, N, et P les projetés orthogonals de O sur (BC), (AC), et (AB).
Posons OM=ON=OP=r.
On a le triangle OMC rectangle en M.
Donc, selon le théorème de pytagore OM²+MC²=OC².
Donc r²+MC²=OC².
De même r²+NC²=OC².
D'où on déduit que r²+MC²=r²+NC².
Donc MC²=NC².
Donc MC=NC.==>(1)
De la même manière, on prouve que AP=AN.==>(2)
De 1 et 2, on trouve que AN+NC=AP+MC.
Donc AC=AP+MC.
Revenons à notre exercice:
On a supposé que AD+CE=AC.
En utilisant ce que je viens de démontrer,
On trouve que E et D sont les projetés respectifs de O sur (AB) et (BC).
(Je ne suis pas sur qu'à 90 pour cent de ce que j'ai dit -en dessinant plusieurs figures, j'ai remarqué que la distance entre le point d'intersection de la bissectrice et le projeté orthogonal sur [BC] ne peut pas être la même sur [AB] que s'ils sont le même point-).
Notons O le point d'intersection de (CD) et (AE).
Posons ECO=c et OAC=a. (angles)
On trouve directement que BAC=2a et ACB=2c. (angles)
La somme des mesures des angles d'un triangle vaut 180°.
Donc ABC+ACB+BAC=180°. (angles)
Donc ABC+2c+2a=180°. (angles)
Donc ABC+2(c+a)=180°. (angles)
Donc ABC=180°-2(c+a).==>(3) (angles)
On a le triangle DAC rectangle en D.
Donc DAC+ACD=90°. (angles)
Donc 2a+c=90°.==>(4) (angles)
De même, on aboutit à 2c+a=90°.==>(5) (angles)
En sommant 4 et 5, on trouve que 2a+c+2c+a=90°+90°. (angles)
Donc 3(a+c)=180°. (angles)
Donc a+c=60°. (angles)
En remplaçant dans 3, on trouve ABC=180°-2*60°.
Donc ABC=180°-120°. (angle)
Donc ABC=60°. (angle) Bonjour nmo, aprés de réflichir un peu à ce bon EX, j'ai passé de votre idée, mais j'ai tombé sur le piége de ABC est un triangle équilatéral ! d'aprés les donées cela est faux ! Si cela est vrai, ce qui est en bleu rend votre methode plus loOngue. Si tu peux expliquer votre passage en bleu foncé ca serait bien. Je ne le trouve pas forcément juste en comparaison aux donées.. Merci. | |
|   | | Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Calcul d'angle encore Sujet: Re: Calcul d'angle encore  Sam 12 Juin 2010, 15:29 Sam 12 Juin 2010, 15:29 | |
|  ) est la bissectrice de 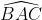 et E appartient au segment [BC], donc 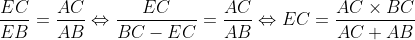 . De même en considérant la bissectrice (CD), 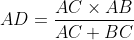 . En additionnant, il vient que : (AC+BC)%20=%20BC(AC+BC)%20+%20AB(AC+AB)%20\Leftrightarrow%20AB\times%20BC%20+%20AC^2%20=%20AB^2%20+%20BC^2) . Or, 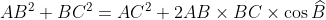 d'après le théorème d'Al-Kashi. De fait : 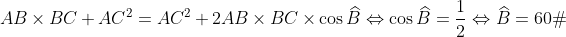 . | |
|   | | M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Calcul d'angle encore Sujet: Re: Calcul d'angle encore  Sam 12 Juin 2010, 17:28 Sam 12 Juin 2010, 17:28 | |
| - Dijkschneier a écrit:

) est la bissectrice de est la bissectrice de 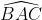 et E appartient au segment [BC], donc et E appartient au segment [BC], donc 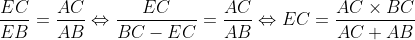 . .
De même en considérant la bissectrice (CD), 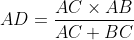 . .
En additionnant, il vient que :
(AC+BC)%20=%20BC(AC+BC)%20+%20AB(AC+AB)%20\Leftrightarrow%20AB\times%20BC%20+%20AC^2%20=%20AB^2%20+%20BC^2) . .
Or, 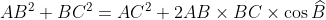 d'après le théorème d'Al-Kashi. d'après le théorème d'Al-Kashi.
De fait : 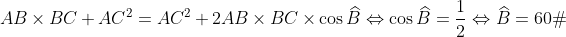 . . Bien joué dijksheiner, belle methode. Pas la peine de poster une autre réponse qui consiste à utiliser le theoréme de bessectrices intérieurs ( CE/EB=BD/AD et: AE²=BD*AD[1-(AC/(BD+AD))²]. Puis: AC/AD=BC/BC et: AC/CE=AB/EB (en considérant une droite paralléle à l'une des bissectrices). (BC/BD -1)(AB/EB -1)=1 Et puis utiliser Alkashi on trouvera B=60°. [J'ai trouvé aussi: AC²=AB*BC et ça sera trés utille]. Merci. | |
|   | | houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: Calcul d'angle encore Sujet: Re: Calcul d'angle encore  Sam 12 Juin 2010, 23:33 Sam 12 Juin 2010, 23:33 | |
| salam
très belle démonstration de Dijkschneier
.................... | |
|   | | nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Calcul d'angle encore Sujet: Re: Calcul d'angle encore  Mar 15 Juin 2010, 11:53 Mar 15 Juin 2010, 11:53 | |
| - M.Marjani a écrit:
- nmo a écrit:
- Laissons l'exercice à part quelque temps:
Soit ABC un triangle et soit O le point d'intersection des bissectrices intérieures (le centre de son cercle inscrit).
Soit M, N, et P les projetés orthogonals de O sur (BC), (AC), et (AB).
Posons OM=ON=OP=r.
On a le triangle OMC rectangle en M.
Donc, selon le théorème de pytagore OM²+MC²=OC².
Donc r²+MC²=OC².
De même r²+NC²=OC².
D'où on déduit que r²+MC²=r²+NC².
Donc MC²=NC².
Donc MC=NC.==>(1)
De la même manière, on prouve que AP=AN.==>(2)
De 1 et 2, on trouve que AN+NC=AP+MC.
Donc AC=AP+MC.
Revenons à notre exercice:
On a supposé que AD+CE=AC.
En utilisant ce que je viens de démontrer,
On trouve que E et D sont les projetés respectifs de O sur (AB) et (BC).
(Je ne suis pas sur qu'à 90 pour cent de ce que j'ai dit -en dessinant plusieurs figures, j'ai remarqué que la distance entre le point d'intersection de la bissectrice et le projeté orthogonal sur [BC] ne peut pas être la même sur [AB] que s'ils sont le même point-).
Notons O le point d'intersection de (CD) et (AE).
Posons ECO=c et OAC=a. (angles)
On trouve directement que BAC=2a et ACB=2c. (angles)
La somme des mesures des angles d'un triangle vaut 180°.
Donc ABC+ACB+BAC=180°. (angles)
Donc ABC+2c+2a=180°. (angles)
Donc ABC+2(c+a)=180°. (angles)
Donc ABC=180°-2(c+a).==>(3) (angles)
On a le triangle DAC rectangle en D.
Donc DAC+ACD=90°. (angles)
Donc 2a+c=90°.==>(4) (angles)
De même, on aboutit à 2c+a=90°.==>(5) (angles)
En sommant 4 et 5, on trouve que 2a+c+2c+a=90°+90°. (angles)
Donc 3(a+c)=180°. (angles)
Donc a+c=60°. (angles)
En remplaçant dans 3, on trouve ABC=180°-2*60°.
Donc ABC=180°-120°. (angle)
Donc ABC=60°. (angle) Bonjour nmo, aprés de réflichir un peu à ce bon EX, j'ai passé de votre idée, mais j'ai tombé sur le piége de ABC est un triangle équilatéral ! d'aprés les donées cela est faux ! Si cela est vrai, ce qui est en bleu rend votre methode plus loOngue.
Si tu peux expliquer votre passage en bleu foncé ca serait bien. Je ne le trouve pas forcément juste en comparaison aux donées..
Merci. En fait, il s'agit de comparer ce que j'ai démontrer avec le fait de supposer que AD+CE=AC. Plus simplement, il faut établir l'équivalence entre les phrases suivantes: Soit ABC un triangle et soit O le point d'intersection des bissectrices intérieures (le centre de son cercle inscrit). Soit M, N, et P les projetés orthogonals de O sur (BC), (AC), et (AB). *CB=CN+BP. *(CP) est perpendiculair à (AB) et (CN) est perpendiculaire à (BN). Comme tu vois j'ai passé de la deuxième à la première. Il me reste le réciproque et c'est fini, je vais essayer encore plus tard. Je pense aussi que ça ne marche pas que si ce qui est en rouge est réalisé. Au plaisir.
Dernière édition par nmo le Lun 20 Sep 2010, 17:24, édité 1 fois (Raison : Faute de frappe) | |
|   | | creep001
Débutant
 Nombre de messages : 3 Nombre de messages : 3
Age : 28
Date d'inscription : 05/09/2010
 |  Sujet: Re: Calcul d'angle encore Sujet: Re: Calcul d'angle encore  Lun 20 Sep 2010, 17:14 Lun 20 Sep 2010, 17:14 | |
| | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Calcul d'angle encore Sujet: Re: Calcul d'angle encore  | |
| |
|   | | | | Calcul d'angle encore |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
