| | Equation |  |
|
|
| Auteur | Message |
|---|
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Equation Sujet: Equation  Sam 21 Aoû 2010, 00:15 Sam 21 Aoû 2010, 00:15 | |
| Résoudre dans  l'équation suivante :  | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Equation Sujet: Re: Equation  Sam 21 Aoû 2010, 02:54 Sam 21 Aoû 2010, 02:54 | |
| Bonsoir tout le monde  D'abord , je te remercie Othman pour cette jolie équation  voilà ma modeste solution   Sauf erreur biensur  | |
|
  | |
Math=life
Maître
 Nombre de messages : 105 Nombre de messages : 105
Age : 33
Date d'inscription : 12/02/2010
 |  Sujet: Re: Equation Sujet: Re: Equation  Sam 21 Aoû 2010, 03:18 Sam 21 Aoû 2010, 03:18 | |
| @tarask:
Les 3 dernieres congruences sont 3 cas parmi plusieurs autre ( plus que 3)
T'a oublié par exemple le cas ou:
x^3+y^3+z^3 = 3 (mod 4) | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Equation Sujet: Re: Equation  Sam 21 Aoû 2010, 03:20 Sam 21 Aoû 2010, 03:20 | |
| - Math=life a écrit:
- @tarask:
Les 3 dernieres congruences sont 3 cas parmi plusieurs autre ( plus que 3)
T'a oublié par exemple le cas ou:
x^3+y^3+z^3 = 3 (mod 4) mais c'est le même que x^3+y^3+z^3=-1(mod4) retranche le 4 !  Gentiment  | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Equation Sujet: Re: Equation  Sam 21 Aoû 2010, 03:21 Sam 21 Aoû 2010, 03:21 | |
| 3=-1 (mod 4)
La méthode me semble juste , avant de conclure tu pouvais simplement dire que 2002=2 (mod4).
Ce n'est pas l'unique méthode , j'attends tjr d'autres reponses.
EDIT : euh non il y'a bien une erreur si on prend x^3=0[mod4] y^3=z^3=1[mod4] ...
Dernière édition par Othmaann le Sam 21 Aoû 2010, 03:28, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Equation Sujet: Re: Equation  Sam 21 Aoû 2010, 03:24 Sam 21 Aoû 2010, 03:24 | |
| Laborieux. x,y,z <= 2002^(1/3), et par conséquent, x,y,z <= 12. On peut alors tester tous les triplets possibles par force brute. 12^3 cas à étudier dans le pire des cas, mais peut être affiné en ôtant les cas inutiles en raison de la symétrie. Pour encore plus de contraintes, on peut étudier les résidus modulo 7 des cubes : un cube ne peut prendre que trois résidus modulo 7 : 0, 1 et -1. Puisque 2002 est un multiple de 7, alors soit tout est congru à 0 modulo 7, soit par symétrie des rôles, on doit bien avoir que x^3 est congru à 0 modulo 7, y^3 à -1 modulo 7, et z^3 à 1 modulo 7. Mais x^3 ne peut avoir un résidu nul modulo 7 que si x a un résidu nul modulo 7. De fait, x=7 ou bien x=0. Et le problème se simplifie à deux variables : 12^2 dans le pire des cas, mais 72 cas en pratique. Peut être amélioré. @Tarask : x^3 + y^3 + z^3 peut être congru à 2 modulo 4 
Dernière édition par Dijkschneier le Sam 21 Aoû 2010, 16:28, édité 1 fois | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Equation Sujet: Re: Equation  Sam 21 Aoû 2010, 03:32 Sam 21 Aoû 2010, 03:32 | |
| - Othmaann a écrit:
- 3=-1 (mod 4)
La méthode me semble juste , avant de conclure tu pouvais simplement dire que 2002=2 (mod4).
Ce n'est pas l'unique méthode , j'attends tjr d'autres reponses.
EDIT : euh non il y'a bien une erreur si on prend x^3=0[mod4] y^3=z^3=1[mod4] ... Oui malheureusement , c'est ce que vient de mentionner Dijkschneier  | |
|
  | |
houssam16
Habitué
 Nombre de messages : 11 Nombre de messages : 11
Age : 31
Localisation : Tetouan
Date d'inscription : 17/08/2010
 |  Sujet: Re: Equation Sujet: Re: Equation  Sam 21 Aoû 2010, 16:23 Sam 21 Aoû 2010, 16:23 | |
| voila une simple methode
on 4(ab)^3+4(bc)^3+4(ac)^3= (a^3+b^3+c^3)^2 -(a^3-b^3-c^3)^2
=(2a^3)(2b^3+2c^3) donc bc^3=0 et ça donne (b=0 ou a=0)
ou suppose que c=0 alors a^3+b^3=2002 ========) (a et b paire ) ou (a et b impaire)
on suppose que a=2x et b=2x =========) x^3+y^3=2002/8 impossible parce que
( x et y)£N
et on 13^3 plus grand que 2002 alors (a et b )£ (1.3.5.7.9.11) et on
2002 plus grand et (8^3+11^3 ) plus grand que (1^3+3^3) .(3^3+5^3)..................... sauf que 11^3+9^3 c'est le seul nombre dans cet ensemble grand que 2002
et on 11^3+9^3=2060
si a=b ====) 2a^3=2002 ====) a^3=1001 ======) a n'appartient pas en N
alors il n'y a aucun solutions pour équations
ps : bc=0 on peut trouver que b=0 et c=0 ========) a3=2002
A+ | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Equation Sujet: Re: Equation  Sam 21 Aoû 2010, 18:45 Sam 21 Aoû 2010, 18:45 | |
| Je n'ai pas très bien compris ta solution. - Citation :
- voila une simple methode
on 4(ab)^3+4(bc)^3+4(ac)^3= (a^3+b^3+c^3)^2 -(a^3-b^3-c^3)^2
=(2a^3)(2b^3+2c^3) donc bc^3=0 et ça donne (b=0 ou a=0) Je ne vois déjà pas la relation entre ce début de démonstration et le problème. Ensuite il y'a une une erreur car (a^3+b^3+c^3)^2 -(a^3-b^3-c^3)^2 = 4(ab)^3 + 4(ac)^3. Sois plus explicite stp. | |
|
  | |
houssam16
Habitué
 Nombre de messages : 11 Nombre de messages : 11
Age : 31
Localisation : Tetouan
Date d'inscription : 17/08/2010
 |  Sujet: Re: Equation Sujet: Re: Equation  Sam 21 Aoû 2010, 23:32 Sam 21 Aoû 2010, 23:32 | |
| ok
on a 2002^2=(a^3+b^3+c^3)^2 ====)2002^2-(a^3-b^3-c^3)^2=(a^3+b^3+c^3)^2-(a^3-b^3-c^3)^2
====) (2002-a^3+b^3+c^3)(2002+(a^3-b^3-c^3))=(4(ab)^3+4(bc)^3+4(ac)^3)
et on a 2002= a^3+b^3+c^3
(2002-a^3+b^3+c^3)(2002^2+(a^3-b^3-c^3))= (2b^3+2c^3)(2a^3)
====) (4(ab)^3+4(bc)^3+4(ac)^3= 4(ab)^3+4(bc)^3 donc bc=0 | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Equation Sujet: Re: Equation  Dim 22 Aoû 2010, 04:07 Dim 22 Aoû 2010, 04:07 | |
| Je n'arrive pas très bien à suivre comme ça, ca me parait assez laborieux tout de meme. Si tu pouvais écrire en Latex ca serait bcp mieux. Et aussi garder les notations (x,y,z) de lexercice.
Désolé pour le dérangement mais c'est pénible comme ça. Je posterai une solution demain , très proche de celle de Dijkschneier. | |
|
  | |
Othman24
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 32
Date d'inscription : 23/07/2010
 |  Sujet: Re: Equation Sujet: Re: Equation  Mar 24 Aoû 2010, 14:59 Mar 24 Aoû 2010, 14:59 | |
| Houssam 16
POURQUOI bc=0 ?? | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Equation Sujet: Re: Equation  Mar 24 Aoû 2010, 15:09 Mar 24 Aoû 2010, 15:09 | |
| - Othman24 a écrit:
- Houssam 16
POURQUOI bc=0 ?? Bonjour othman24 , je crois que toute la démarche de Houssam est fausse (no offense  ) je m'explique : - houssam16 a écrit:
- voila une simple methode
on 4(ab)^3+4(bc)^3+4(ac)^3= (a^3+b^3+c^3)^2 -(a^3-b^3-c^3)^2
=(2a^3)(2b^3+2c^3) donc bc^3=0 et ça donne (b=0 ou a=0)
ou suppose que c=0 alors a^3+b^3=2002 ========) (a et b paire ) ou (a et b impaire)
on suppose que a=2x et b=2x =========) x^3+y^3=2002/8 impossible parce que
( x et y)£N
et on 13^3 plus grand que 2002 alors (a et b )£ (1.3.5.7.9.11) et on
2002 plus grand et (8^3+11^3 ) plus grand que (1^3+3^3) .(3^3+5^3)..................... sauf que 11^3+9^3 c'est le seul nombre dans cet ensemble grand que 2002
et on 11^3+9^3=2060
si a=b ====) 2a^3=2002 ====) a^3=1001 ======) a n'appartient pas en N
alors il n'y a aucun solutions pour équations
ps : bc=0 on peut trouver que b=0 et c=0 ========) a3=2002
A+ Rouge : pas du tout clair Vert : au début tu supposes que c=0 alors directement tu as bc=0 , en plus pourquoi tu n'as pas traité le cas de c=/ 0 ? Bleu: t'as traité un seul cas de parité ... de plus , a=2x et b=2x le x est indépendant de celui traité dans l'exercice  Amicalement  et dsl si je n'ai pas bien compris votre solution ..... | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Equation Sujet: Re: Equation  Mar 24 Aoû 2010, 23:58 Mar 24 Aoû 2010, 23:58 | |
| Donc comme dit ci-dessus voici ma solution : on a : 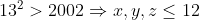 on aussi : \Rightarrow%20x^3+y^3+z^3\equiv%200(mod7)) En dressant un tableau de congruence on peut remarquer que les seuls résidus d'un cube modulo 7 sont : 0 , 1 et -1 Il est donc obligatoire qu'au moins ) ou ) ou ) (toujours pas tableau de congruence) Par symétrie des rôles on suppose que \Rightarrow%20z\equiv%200(7)) et comme 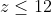 alors z=0 ou z=7 cas 1: z=0 L'équation devient : 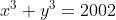 Encore une fois d'après les résidus modulo 7. ) ou %20&%20\\%20y^3\equiv%20-1(7)%20&%20\end{matrix}\right.) On remarque que : ;(0,7);(7,0);(7,7)) ne sont pas des solutions. Donc %20&%20\\%20y^3\equiv%20-1(7)%20&%20\end{matrix}\right.) Il me semble qu'on a réduit les possibilités au maximum il ne reste plus qu'a essayer les nombres , alors : ) ) Soit S l'ensemble de solution de l'equation. 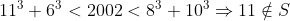 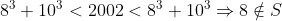 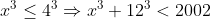 Donc dans ce cas l'équation n'admet aucune solution. La même méthode est réalisable quand z=7. Et on ne trouve également aucune solution. Donc 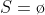 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Equation Sujet: Re: Equation  | |
| |
|
  | |
| | Equation |  |
|
