Une inégalité faisant intervenir des nombres premiers

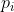Montrer que : , où désigne le ième nombre premier.

Il faut juste utiliser le postulat de Bertrand :

Le reste est assez simple .

Bien Sylphaen.
Solution complète :
Démontrons ce résultat par récurrence.
Soit P(n) la fonction propositionnelle définie par :
- Initialisation : P(1) : 2 + 1 >= 3 est vraie
- Hérédité :
Supposons que P(n) est vraie. Montrons que P(n+1) l'est aussi.
P(n) est vraie

Il s'agit donc de montrer que . Mais puisque d'après le postulat de Bertrand, on a , alors il suffit de montrer que , qui est équivalente à , qui est sans entrer dans les détails, vraie.
Ainsi, P(n+1) est vraie aussi.
Fin de la récurrence.

Plus simple!
1+produit(p_i,i=1..n) admet un diviseur premier q différent de p_i,i=1..n, donc q>= p_n+1 !!

Bien m.elouafi.

Il me semble que c'est le même raisonnement , le théorème qu'a utilisé M.elouafi n'est qu'une autre formulation du postulat de Bertrand et c'est le théorème de Sylvester.

J ai simplement utilisé le théorème fondamentale d'arithmétique:
" Chaque entier >= 2 admet un diviseur premier "

Merci de confirmer les propos de m.elouafi.

Dijkschneier a écrit:

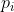Montrer que : , où désigne le ième nombre premier.

la suite logique :
deduire que le nieme nombre premier est inferieur à log(log(n))

le log(x) = ln(x)/ln(2) : log en base 2!

Citation :

J ai simplement utilisé le théorème fondamentale d'arithmétique:
" Chaque entier >= 2 admet un diviseur premier "

y a pas de demonstration plus elegante que cella

béhé a écrit:

la suite logique :
deduire que le nieme nombre premier est inferieur à log(log(n))
le log(x) = ln(x)/ln(2) : log en base 2!

Ça doit être : "supérieur".
Ceci est équivalent à , ce qui est évidemment vrai par récurrence, puisque p_(n+1) >= p_n pour tout entier n.
Je crois que tu ne nous as pas bien fait partager l'énoncé : je soupçonne que l'énoncé correct demande de prouver une inégalité sur la fonction PI qui compte les nombres premiers.