Sporovitch
Maître
 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 | | Sujet: Nouvelle (own) Mer 15 Sep 2010, 15:40 | |
| Soient a,b,c des réels positifs tels que a+b+c>= abc on pose a²+b²+c²=x et abc=y MQ:  | |
|
majdouline
Expert sup
 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
| | Sujet: Re: Nouvelle (own) Jeu 16 Sep 2010, 09:14 | |
| bonjour...... l'inégalité est équivalente à : 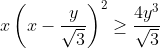 remarquons qu'il suffit de montrer que : 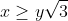 , Or :  ce qui achève la preuve! | |
|
Sporovitch
Maître
Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
| | Sujet: Re: Nouvelle (own) Jeu 16 Sep 2010, 13:05 | |
| Saluut that's it  Bravo  | |
|
Sporovitch
Maître
Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
| | Sujet: Re: Nouvelle (own) Jeu 16 Sep 2010, 18:17 | |
| Une autre inégalité crée a l'aide de mon ami (KING) : soient a,b,c >=0 et x,y,z £ IR MQ: 2(a²+b²+c²+ab+bc+ac)(x²+y²+z²+xy+yz+xz)>=(a+b)²(x²+2yz)+(b+c)²(y²+2xz)+(a+c)²(z²+2xy) Bonne chance  | |
|
Contenu sponsorisé
| | Sujet: Re: Nouvelle (own) | |
| |
|
