hamza15
Habitué
 Nombre de messages : 12 Nombre de messages : 12
Age : 28
Date d'inscription : 05/10/2010
 |  Sujet: help Sujet: help  Mer 06 Oct 2010, 12:55 Mer 06 Oct 2010, 12:55 | |
| a , b et c appartient à IR différent deux à deux
montré que
1/(a-b)(a-c) + 1/(b-c)(b-a) + 1/(c-a)(c-b)=0
trouvé que
a+b/(b-c)(c-a) + b+c/(c-a)(a-b)=a+c/(b-a)(b-c)
Dernière édition par hamza15 le Jeu 28 Oct 2010, 13:40, édité 1 fois | |
|
hamza15
Habitué
 Nombre de messages : 12 Nombre de messages : 12
Age : 28
Date d'inscription : 05/10/2010
 |  Sujet: Re: help Sujet: Re: help  Mer 06 Oct 2010, 20:38 Mer 06 Oct 2010, 20:38 | |
| | |
|
hamza15
Habitué
 Nombre de messages : 12 Nombre de messages : 12
Age : 28
Date d'inscription : 05/10/2010
 |  Sujet: Re: help Sujet: Re: help  Jeu 07 Oct 2010, 13:26 Jeu 07 Oct 2010, 13:26 | |
| je trouve la solution merci | |
|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: help Sujet: Re: help  Mar 12 Oct 2010, 11:30 Mar 12 Oct 2010, 11:30 | |
| - hamza15 a écrit:
- a , b et c appartient à IR différent deux à deux
montré que
1/(a-b)(a-c) + 1/(b-c)(b-a) + 1/(c-a)(c-b)=0
trouvé que
a+b/(b-c)(c-a) + b+c/(c-a)(a-b)=a+c/(b-a)(b-c) Pour le premier: Posons (a-c)}+\frac{1}{(b-c)(b-a)}+\frac{1}{(c-a)(c-b)}) . Donc (c-a)}+\frac{-1}{(b-c)(a-b)}+\frac{-1}{(c-a)(b-c)}) . Donc }{(a-b)(b-c)(c-a)}+\frac{-(c-a)}{(b-c)(a-b)(c-a)}+\frac{-(a-b)}{(c-a)(b-c)(a-b)}) . Donc -(c-a)-(a-b)}{(a-b)(b-c)(c-a)}) . Donc (b-c)(c-a)}) . Donc (b-c)(c-a)}) . Donc 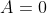 . Pour le deuxième: On a (a-c)}+\frac{1}{(b-c)(b-a)}+\frac{1}{(c-a)(c-b)}=0) . Donc (a-c)}+\frac{1}{(c-a)(c-b)}=\frac{-1}{(b-c)(b-a)}) . Donc (a-c)}+\frac{-a-c}{(c-a)(c-b)}=\frac{a+c}{(b-c)(b-a)}) . Donc (c-a)}+\frac{a+c}{(c-a)(b-c)}=\frac{a+c}{(b-c)(b-a)}) . Donc (c-a)}+\frac{a}{(a-b)(c-a)}+\frac{a}{(c-a)(b-c)}+\frac{c}{(c-a)(b-c)}=\frac{a+c}{(b-c)(b-a)}) . Pour qu'on aille le résulta, il faut que (c-a)}+\frac{b}{(c-a)(b-c)}=\frac{a}{(a-b)(c-a)}+\frac{c}{(c-a)(b-c)}) . Pour simplifier, on multiplie par (c-a). On touve 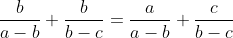 . Prouvons ce résultat: On a 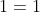 . Donc 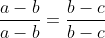 . Donc 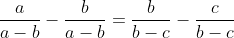 . Donc 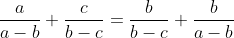 . Ce qui met fin à la preuve. CQFD. | |
|
