| | irationalité de racine 3 |  |
|
+6Bison_Fûté nmo Mim master amazigh-tisffola lobna 10 participants |
| Auteur | Message |
|---|
lobna
Débutant
 Nombre de messages : 5 Nombre de messages : 5
Age : 32
Date d'inscription : 17/10/2010
 |  Sujet: irationalité de racine 3 Sujet: irationalité de racine 3  Dim 17 Oct 2010, 15:11 Dim 17 Oct 2010, 15:11 | |
| Bonjour, j'espère que quelqu'un pourra m'aider a resoudre mon exercice? svp ,Démontrer que racine carré de 3 est irrationnel
comme l racine 2 j' utilise la raisonnoment par l'absurde;mais j' arretra à p2=3q2
je vous remercie d'avance..... | |
|
  | |
Invité
Invité
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  Dim 17 Oct 2010, 19:20 Dim 17 Oct 2010, 19:20 | |
| |
|
  | |
amazigh-tisffola
Expert grade1

 Nombre de messages : 487 Nombre de messages : 487
Age : 40
Localisation : kelaa m'gouna
Date d'inscription : 01/10/2010
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  Dim 17 Oct 2010, 19:41 Dim 17 Oct 2010, 19:41 | |
| v3£/Q car il n'existe pas un m£IN tel que 3=m^2
en effet 3=m^2 ==>1<m^2<4 ==>1<m<2 absurde puisque m£IN;
PROPRIETE GENERALE:
qlq soit n£IN vn£Q <==> vn£IN
preuve:
<== ok
==> si vn=p/q alors q^2n=p^2 et donc q^2/p^2 <==>q^2/p^2*1 or pgcd(q^2,p^2)=1
==>par gauss q^2/1 ==>q^2=1 | |
|
  | |
lobna
Débutant
 Nombre de messages : 5 Nombre de messages : 5
Age : 32
Date d'inscription : 17/10/2010
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  Dim 17 Oct 2010, 20:38 Dim 17 Oct 2010, 20:38 | |
| j'ai djà la montré : p n' est pas divisible par 3=>p=3k+1 ou p=3k+2 =>p²=(3K+1)² ou p²=(3k+2)² =>p²=3(3k²+2k)+1 ou p²=3(3k²+4k+1)+1 =>p² n'est pas divisible par 3 et merci  | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  Dim 17 Oct 2010, 22:04 Dim 17 Oct 2010, 22:04 | |
| slm , ou bien avec les valuations p-adique !
v_3(V3)+v_3(V3)=2.v_3(V3)=1 ==> v_3(V3)=1/2 ==> cela n'est pas possible puisque les valuations p-adiques sont toujours entiers . | |
|
  | |
Mim
Maître
 Nombre de messages : 165 Nombre de messages : 165
Age : 29
Date d'inscription : 06/05/2010
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  Jeu 28 Oct 2010, 21:27 Jeu 28 Oct 2010, 21:27 | |
| - amazigh-tisffola a écrit:
PROPRIETE GENERALE:
qlq soit n£IN vn£Q <==> vn£IN
preuve:
<== ok
==> si vn=p/q alors q^2n=p^2 et donc q^2/p^2 <==>q^2/p^2*1 or pgcd(q^2,p^2)=1
==>par gauss q^2/1 ==>q^2=1 Ta propriété est trop trop intéréssante  , pourrais tu m'expliquer ce que j'ai souligné en rouge ? ( deja je pense que tu voulais mettre p^2 / q^2 et après je n'ai pas compris le *1 que tu as fais , bref j'aimerai avoir des éclaircissement afin de pouvoir utiliser cette propriété durant l'examen | |
|
  | |
amazigh-tisffola
Expert grade1

 Nombre de messages : 487 Nombre de messages : 487
Age : 40
Localisation : kelaa m'gouna
Date d'inscription : 01/10/2010
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  Jeu 28 Oct 2010, 21:47 Jeu 28 Oct 2010, 21:47 | |
| salam Mim,
on fait j'ai rien changer, juste multiplie le dénominateur par 1, c'et a dire (p^2)*1 , comme q^2 devise p^2 et pgcd(q^2,p^2)=1 ==>q^2/1.
q^2/p^2 <==>q^2/(p^2)*1
propriété de Gauss:
soit a, b et c des entiers,
si pgcd(a,b)=1 c'est a dire a et b sont premier entre eux et c'est a devise bc on écrit a/bc alors adevise c ( a/c)
ps:le c dans l'exercice c'est 1 | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  Ven 05 Nov 2010, 12:59 Ven 05 Nov 2010, 12:59 | |
| Même si ce n'est pas la rubrique apropriée, je profite de cette discussion pour présenter une de mes qustions: Afin de démontrer que  , on suit la procédure suivante: On a  et  . Donc  . Et  . Que penseez vous? | |
|
  | |
Bison_Fûté
Expert sup

 Nombre de messages : 1595 Nombre de messages : 1595
Age : 65
Date d'inscription : 11/02/2007
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  Ven 05 Nov 2010, 13:08 Ven 05 Nov 2010, 13:08 | |
| BJR nmo !!
Je voulais seulement te faire remarquer que tu fais là une erreur SOURNOISE de LOGIQUE !!
Je t'en donne un exemple et tu comprendras :
1+rac(2) n'est pas dans Q
de même
1-rac(2) n'est pas dans Q
MAIS leur produit {1+rac(2)}.{1-rac(2)}=1-2=-1 est dans Q
A méditer alors .....
Amicalement . LHASSANE | |
|
  | |
Bison_Fûté
Expert sup

 Nombre de messages : 1595 Nombre de messages : 1595
Age : 65
Date d'inscription : 11/02/2007
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  Ven 05 Nov 2010, 17:31 Ven 05 Nov 2010, 17:31 | |
| - lobna a écrit:
- Bonjour, j'espère que quelqu'un pourra m'aider a resoudre mon exercice? svp ,Démontrer que racine carré de 3 est irrationnel
comme l racine 2 j' utilise la raisonnoment par l'absurde;mais j' arretra à p2=3q2
je vous remercie d'avance..... BJR à Vous Toutes et Tous !! En parcourant ce Topic , Je me suis aperçu que les Contributeurs avaient proposé des solutions basées sur des arguments divers ... Le Théorème de GAUSS , quoique répondant à la question , n'est pas du niveau Lycée ( même BACSM ) !! C'est un résultat très fort . Par contre , j'ai eu quelque idée qui rejoint en force celle de salimt . Elle mérite d'être développée ...... On arrive à p^2=3.q^2 si on suppose rac(3)=p/q avec p,q entiers PREMIERS ENTRE EUX et q>=1 ; On déduit d'abord que 3 DIVISE p^2 . Si on raisonnait Modulo 3 !!!!! Si p=0 Modulo 3 alors p=3.k avec k entier donc p^2=9.k^2 et il n'y a aucun problème .... Si p=1 Modulo 3 alors p=3.k+1 et de là p^2=3.{3.k^2 + 2.k}+1 et donc 3 ne divise pas p^2 Si p=2 Modulo 3 alors p=3.k+2 et de là p^2=3.{3.k^2 + 4.k+1}+1 et donc 3 ne divise pas p^2 En définitive , le seul cas ou 3 DIVISE p^2 est le cas ou 3 DIVISE p Donc l'entier p est de la forme 3.k avec k entier et p^2=9.k^2=3.q^2 Une petite simplification donnera 3.k^2=q^2 et ainsi 3 DIVISE cette fois q^2 Par le même raisonnement que précédemment , on en déduit que 3 DIVISE q Et si 3 DIVISE p et 3 DIVISE q alors la fraction (p/q) ne serait plus IRREDUCTIBLE et c'est là l'absurdité !! Amicalement . LHASSANE PS : Merci à salimt .... | |
|
  | |
hindou11
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 32
Date d'inscription : 28/03/2009
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  Dim 14 Nov 2010, 13:55 Dim 14 Nov 2010, 13:55 | |
| ne pourrait-on pas utiliser le carré parfait? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  Dim 14 Nov 2010, 18:04 Dim 14 Nov 2010, 18:04 | |
| - hindou11 a écrit:
- ne pourrait-on pas utiliser le carré parfait?
Je pense que c'est possible, voici une autre solution: Je procède par absurde: Supposons que  . On a  . Donc, il existe (x,y) un couple d'entiers relatifs (y#0), tel que 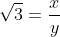 et =1) . Donc 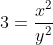 . Donc 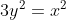 . Donc 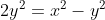 . Donc (x+y)=2y^2) .==>(1) Donc (x+y)) est pair. Or, il est très connu que 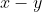 et 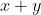 ont la même parité. Ainsi 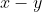 et 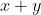 sont pairs.==>(2) D'où l'existance de deux eniers relatifs a et b tel que x-y=2a et x+y=2b. Donc 1 équivaut à dire que 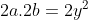 . Donc 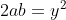 . Donc 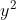 est pair. Or, y et 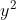 ont la même parité. D'où y est pair.==>(3) En vertu de 2, il vient que x est pair.==>(4) Remarquons que 3 et 4 prouvent que \neq1) . En contradiction avec l'hypothèse. Donc  . | |
|
  | |
Heikichi
Féru
 Nombre de messages : 37 Nombre de messages : 37
Age : 28
Date d'inscription : 07/10/2011
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  Jeu 15 Nov 2012, 12:55 Jeu 15 Nov 2012, 12:55 | |
| Oui mais petit problème sur ta démonstration , (x-y)(x+y ) =2y² Faut signaler que x > y . Or on a pas cette donnée  Ps : Désolé D'avoir remonter un topic aussi lointain mais sa me démangeait de savoir ça ;. | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  Jeu 15 Nov 2012, 18:40 Jeu 15 Nov 2012, 18:40 | |
| @Heikichi
Dans cette démonstration on a précédemment signalé que 3=x²/y² | |
|
  | |
generale
Débutant
 Nombre de messages : 1 Nombre de messages : 1
Age : 30
Date d'inscription : 15/11/2012
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  Jeu 15 Nov 2012, 19:47 Jeu 15 Nov 2012, 19:47 | |
| démonstration par l'absurde. On écrit racine3=a/b avec (a,b)£R+ d'où 3=a2/b2. On démontre ainsi que 3/a et 3/b d'où pgcd(a,b)#1 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: irationalité de racine 3 Sujet: Re: irationalité de racine 3  | |
| |
|
  | |
| | irationalité de racine 3 |  |
|
