utile

Bonjour.
Soit f une fonction (définie dans R et à valeurs dans R) dérivable et 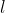un réel. Montrer que :
1/.

2/.

Étudier l'implication réciproque dans les deux cas (par un contre-exemple ou une démonstration).
P.S: C'est très intuitive mais la démonstration ne l'est pas autant. C'est surtout que c'est très utile ce genre de lemme.
Bonne découverte.

Bonjour
Je relance le sujet , peut-être que cette fois-ci il intéressera quelqu'un.

c tré interessan en éfé :/ !

saluut tt le monde je vous souhaite aid mobarak said
bon voilà la solution que je propose pour la premiere question
f'(x)-->l (quandx-->+oo)
==>lim(x-->oo) (f(x)-f(x'))/(x-x')=l
==>klksoi epsilon>0 il existe A>0 pr tt x>A==>|(f(x)-f(x'))/(x-x')-l|<epsilon
==>(x-x')(l-epsilon)<f(x)-f(x')<(x-x')(epsilon-l)
==>f(x')/x+ (1-x'/x)(l-epsilon)<f(x)/x<(1-x'/x)(epsilon-l)+f(x')/x
==>f(x')/x+ (1-x'/x)(l-epsilon)-l<f(x)/x - l<(1-x'/x)(epsilon-l)+f(x')/x-l
or quand x-->+oo on a (1-x'/x)(epsilon-l)+f(x')/x-l ---> epsilon
et f(x')/x+ (1-x'/x)(l-epsilon)-l --> -epsilon (car f est continue en x')
==>donc |f(x)/x - l|<epsilon
d'ou le resultat

bonjour
Je n'ai pas lu toute la démonstration , difficile de se concentrer quand cest écrit en vrac comme ça mais surtt que qès la première ligne , je me demande si c'est vraiment ça ??

<< f'(x)-->l (quandx-->+oo)
==>lim(x-->oo) (f(x)-f(x'))/(x-x')=l >>

c'est la définition de la dérivée en un point mais au voisinage de +infini cest bien ça ? quel est le role de x' alors ?

moi aussi je ne suis pas sur de ce que j'ai écrit car vraiment je n'ai pas une idée sur la limite de la dirivée en +oo mais j'ai pensé à f(x)-f(x'))/x-x' comme etant le coefficient directeur de la tangeante en un point x' cela peut avoir une relation avec la dérivée...
j'espere qu'un membre va poster la bonne démonstration car je vois que cette exercice et très intéressant
Amicalement Ayoub.

pour (1)

f'(x) tends vers L quand x tend vers + infinie équivalent à qlq epsilon strictement positive , il existe A>0 , pour tt x de l'ensemble de définition de f : x>A => |f'(x)-L|<epsilon
------------------------------------------------------------------------------------------
soit epsilon >0, pour tout x de Df
x>A => |f'(x)-L|<epsilon
=> L-eps<f'(x)<eps+L
=>x(L-eps)<f(x)<x(eps+L) .....(par l'integrale )
=>L-eps<(f(x))/x<eps+L.....(car x tends vers + infinie)
=>|f(x)/x-L|<epsilon...CQFD

bonsoir

Fermat-X

Ta réponse cache deux problèmes:

1er : On ne sait pas si f ' est intégrable (pas d'hypothèse genre f ' continue ..)

2em: Les bornes d'integration (tu sais bien que l'inégalité est conservée si on intégre entre deux bornes a et b tel que a \leq b )

bon apres une long réfelexion voila ce que j'ai trouvé
en commencera par le cas particulier de L=0
soit eps>0 il existe A>0 tel que pour tout x>A |f'(x)|<eps/2
soit donc x>A (l'inegalité des acroissement fini) appliquée a f entre A et x
|f(x)-f(A)|=<(eps/2)(x-A)
on a alors |f(x)/x|=<|(f(x)-f(A))/x|+|f(A)/x|=<(eps/2)((x-A)/x)+|f(A)/x|
or lim |f(A)/x| en +oo est 0
donc il existe donc B=>A tel que pour tout x>B |f(A)/x|<eps/2
finalement on a montré mnt que pour tout eps>0 il existe B>0 tel que
pour tout x>B |f(x)/x|<eps ce qui est le resultat demandé lorsque L=0
mnt on va generaliser en consideron la fonction defini sur lR par g(x)=f(x)-L.x
on a alors lim g'(x) en +oo = 0 par le premier cas de L=0 on trouve lim f(x)/x en +oo =0 cest a dire que lim f(x)/x=L
est pour le contre exemple de la reciproque on peut considére la fonction cosinus
amicalement math-spirit lml !

est surtout n'esité si vous avé des question je serai a votre ecoute ^^!

bonsoir :

Merci math-spirit pour ta contribution

ici (il suffit de cliquer) se trouve ton travail mis en forme

merci mohameeed c tres gentil de ta part jazaka lahou khayran !
amicalement ^^

math-spirit a écrit:

bon apres une long réfelexion voila ce que j'ai trouvé
en commencera par le cas particulier de L=0
soit eps>0 il existe A>0 tel que pour tout x>A |f'(x)|<eps/2
soit donc x>A (l'inegalité des acroissement fini) appliquée a f entre A et x
|f(x)-f(A)|=<(eps/2)(x-A)
on a alors |f(x)/x|=<|(f(x)-f(A))/x|+|f(A)/x|=<(eps/2)((x-A)/x)+|f(A)/x|
or lim |f(A)/x| en +oo est 0
donc il existe donc B=>A tel que pour tout x>B |f(A)/x|<eps/2
finalement on a montré mnt que pour tout eps>0 il existe B>0 tel que
pour tout x>B |f(x)/x|<eps ce qui est le resultat demandé lorsque L=0
mnt on va generaliser en consideron la fonction defini sur lR par g(x)=f(x)-L.x
on a alors lim g'(x) en +oo = 0 par le premier cas de L=0 on trouve lim f(x)/x en +oo =0 cest a dire que lim f(x)/x=L
est pour le contre exemple de la reciproque on peut considére la fonction cosinus
amicalement math-spirit lml !

merci pour la solution
pas la peine de se montrer genie et faire comme si toi qui as trouvé la solution car tu l'as juste copié

ben merci pour votre commentaire debil sa fait plus de 2 semaine que je cherche la solution et voila que tu débarque toi en me dison que je l'est copié c pas gentil du tout en plus si t'a des source surtout ne te géne pas ! montre les parseke moi je peut t'asuré que c ma propre solution :s !