Dijkschneier
Expert sup
 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 | | Sujet: Une équation fonctionnelle Jeu 03 Fév 2011, 21:16 | |
| Je propose :
Trouver toutes les fonctions f définies sur [0,1] et continues qui soient constantes sur [0,1/2] et qui vérifient f(x)=f(2x-1) sur [1/2,1]
Elle n'est pas difficile. | |
|
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: Une équation fonctionnelle Dim 13 Fév 2011, 01:14 | |
| - Dijkschneier a écrit:
- Je propose :
Trouver toutes les fonctions f définies sur [0,1] et continues qui soient constantes sur [0,1/2] et qui vérifient f(x)=f(2x-1) sur [1/2,1]
Elle n'est pas difficile. Posons :  Nous avons : =f(\frac{y+1}{2})) Soit ) Posons la suite ) telle que 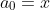 et  Nous avons, \in%20\mathbb{N}^2;f(a_k)=f(a_{k'})) Il est aisé de démontrer par récurrence que  Alors  Il se fait tard, j'ai besoin de dormir. Je pense que la plus grande partie est faite. La solution unique étant la fonction constante. | |
|
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: Une équation fonctionnelle Dim 20 Fév 2011, 18:12 | |
| Oui, bien.
Je suis désolé de n'avoir pas répondu plus tôt.
Je n'avais pas repéré qu'il avait une réponse dans ce topic. | |
|
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: Une équation fonctionnelle Dim 20 Fév 2011, 18:17 | |
| L'idée étant de prouver par récurrence que pour tout n de IN : 0 <= x <= a_n ===> f(x)=constante.
Puis de faire tendre n vers l'infini.
Il en résulte que : 0 <= x < 1 ===> f(x)=constante
Ce qui veut dire : pour tout x de [0,1[, f(x)=constante.
La continuité de f ne sera utile que pour montrer qu'elle vaut également la constante en 1.
Sauf erreur. | |
|
Contenu sponsorisé
| | Sujet: Re: Une équation fonctionnelle | |
| |
|
