| | Equation et trigonométrie: |  |
|
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Equation et trigonométrie: Sam 05 Mar 2011, 18:08 | |
| Voici une équation, de ma création: Résolvez en  l'équation suivante }+2\sin^2{(x)}\big)+2\sin^2{(x)}=0) . Bonne chance. | |
|
| | |
Misterayyoub
Maître
Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
| | Sujet: Re: Equation et trigonométrie: Dim 06 Mar 2011, 18:49 | |
| On peut donner la solution en fonction de sin x ? | |
|
| | |
yasserito
Expert sup
Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
| | Sujet: Re: Equation et trigonométrie: Dim 06 Mar 2011, 18:51 | |
| nn je ne crois pas !y'a une solution je l'ai demontre mais je n'en suis pas sur j'ai trouve x=0 je crois!! | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Equation et trigonométrie: Dim 06 Mar 2011, 19:05 | |
| - yasserito a écrit:
- nn je ne crois pas !y'a une solution je l'ai demontre mais je n'en suis pas sur j'ai trouve x=0 je crois!!
C'est ça, mais je veux la methode. | |
|
| | |
Misterayyoub
Maître
Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
| | Sujet: Re: Equation et trigonométrie: Dim 06 Mar 2011, 19:07 | |
| je ne crois pas que x=0 est la seule solution | |
|
| | |
yasserito
Expert sup
Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
| | Sujet: Re: Equation et trigonométrie: Dim 06 Mar 2011, 19:15 | |
| - Misterayyoub a écrit:
- je ne crois pas que x=0 est la seule solution
jai dis je ne suis pas sur! - nmo a écrit:
- yasserito a écrit:
- nn je ne crois pas !y'a une solution je l'ai demontre mais je n'en suis pas sur j'ai trouve x=0 je crois!!
C'est ça, mais je veux la methode. vous ne l'avez pas resolu vous? je vais recapituler ma methode et je l'envoierai amicalement  | |
|
| | |
Misterayyoub
Maître
Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
| | Sujet: Re: Equation et trigonométrie: Dim 06 Mar 2011, 19:18 | |
| donc il faut resoudre l'equation x²-x(sin(2x) + 2 sin²(x)) +2 sin²(x) =0
pour cela , on peut calculer le descriminant qui egale a :
delta = ( sin(2x) +2sin²(x) )² - 8sin²(x) = ( sin(2x) +2sin²(x) -2v2sin(x) )(sin(2x) +2sin²(x) +2v2sin(x)
avec un peu de cacul on a : delta = 8sin²(x) ( sin(pi/4 +x ) - 1 ) ( sin (pi/4 +x ) +1 )
on etudie le signe du delta , et on a delta positif si , x appartient a ]- linfini ; pi/4 ] union [5pi/4 ; + linfini [ | |
|
| | |
Misterayyoub
Maître
Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
| | Sujet: Re: Equation et trigonométrie: Dim 06 Mar 2011, 19:19 | |
| donc il existe plusieurs solutions en trouvant les x1 et x2 sur le domaine cité | |
|
| | |
Misterayyoub
Maître
Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
| | Sujet: Re: Equation et trigonométrie: Dim 06 Mar 2011, 19:29 | |
| Vous en pensez quoi ?  | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Equation et trigonométrie: Dim 06 Mar 2011, 19:33 | |
| - Misterayyoub a écrit:
- Vous en pensez quoi ?
C'est faux mon cher, on calcule le discriminent si a, b, et c ne dépendent pas de x. Ce n'est pas notre cas ici.
Dernière édition par nmo le Dim 06 Mar 2011, 19:40, édité 1 fois | |
|
| | |
Misterayyoub
Maître
Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
| | Sujet: Re: Equation et trigonométrie: Dim 06 Mar 2011, 19:35 | |
| - nmo a écrit:
- Misterayyoub a écrit:
- Vous en pensez quoi ?
C'est faux mon cher, on calcule le discriminent si a, b, et c se dépendent de x.
Ce n'est pas notre cas ici. Je crois que tu voulais dire , ne dependent pas de x , non ? | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Equation et trigonométrie: Dim 06 Mar 2011, 19:39 | |
| - Misterayyoub a écrit:
- nmo a écrit:
- Misterayyoub a écrit:
- Vous en pensez quoi ?
C'est faux mon cher, on calcule le discriminent si a, b, et c se dépendent de x.
Ce n'est pas notre cas ici. Je crois que tu voulais dire , ne dependent pas de x , non ? Oui, faute de... C'est édité. | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Equation et trigonométrie: Lun 07 Mar 2011, 23:52 | |
| Mystérieuse et belle.. de beaux tournures vraiment. Avant d'écrire ma solution d'une manière concentré, je suggère que s'il y avait d'ambiguïté ou des questions sur quelques passages je vais répondre à bras ouverts. On a A=x^2 -xSin2x -2xSin²x +2Sin²x=0 <==> 2Sin²x[1-x] -2xCosx*Sinx +x^2=0 . Delta=4x²[Cos²x + 2(x-1)]>=0 Pour souhaiter des solutions. Maintenant si D=0 alors soit x=0 soit cos²x=2(1-x) <==> 0<=Sin²x=2x-1=<1 (*) de plus Sinx=-b/2a=2x*cosx/4 <==> 2Sinx=x*Cosx (**) Et par (*) et (**) on déduit que x²cos²x=4(2x-1) et Cos²x=2(1-x). Selon (*) 1/2<=x=<1 et on sait que x>=1/2 => x>1/5 <==> 4(2x-1)>2(x-1) alors x²Cos²x>Cos²x mais 1/2<=x=<1 => [cos²x]/4<=x²*cos²x=<cos²x Contradiction. On suppose maintenant que D>0 alors 0=<Sin²x<2x-1 donc x>=1/2 et selon A=x[x-Sin2x]=2Sin²x[x-1] (***)si x=<1 alors 1/2<=x=<Sin2x=<1 On retombe au premier cas. Maintenant si x>=1 on tire Sin2x=<1<x avec x=1 ne satisfait pas les données donc x différent de 1. Si x>1 alors 1-Sin2x<A=x^2 -xSin2x -2xSin²x +2Sin²x=0 donc Sin2x>1 Contradiction.. Donc S={0}. CQFD.
Dernière édition par M.Marjani le Mar 08 Mar 2011, 12:47, édité 1 fois (Raison : Fautes de frappes) | |
|
| | |
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: Equation et trigonométrie: Mar 08 Mar 2011, 12:37 | |
| - nmo a écrit:
- Voici une équation, de ma création:
Résolvez en l'équation suivante .
Bonne chance. Il suffit de poser f une fonction définie sur IR par : =x^2-x(sin(2x)+2sin^2(x))+2sin^2(x)) Nous avons : =-(2x-1)(sin(2x)+cos(2x)-1)) Un tableau des variations suffit pour affirmer que l'unique solution à l'équation est 0. Enfin... il faut aussi remarquer que : =x^2-x(sin(2x)+2sin^2(x))+2sin^2(x)=x^2-2xsin(x)(sin(x)+cos(x))+(\sqrt2sin(x))^2\geq%20x^2+2x\sqrt2sin(x)+(\sqrt2sin(x))^2=(x-\sqrt2sin(x))^2) Et que de ce fait f(x)>0 pour tout x tel que |x|>\sqrt(2). Le tableau des variations doit donc être fait uniquement sur l'intervalle [-\sqrt(2),\sqrt(2)] Sauf erreur. Au plaisir !
Dernière édition par mizmaz le Mar 08 Mar 2011, 19:13, édité 1 fois | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Equation et trigonométrie: Mar 08 Mar 2011, 19:03 | |
| - M.Marjani a écrit:
Mystérieuse et belle.. de beaux tournures vraiment. Avant d'écrire ma solution d'une manière concentré, je suggère que s'il y avait d'ambiguïté ou des questions sur quelques passages je vais répondre à bras ouverts.
On a A=x^2 -xSin2x -2xSin²x +2Sin²x=0 <==> 2Sin²x[1-x] -2xCosx*Sinx +x^2=0 . Delta=4x²[Cos²x + 2(x-1)]>=0 Pour souhaiter des solutions. Maintenant si D=0 alors soit x=0 soit cos²x=2(1-x) <==> 0<=Sin²x=2x-1=<1 (*) de plus Sinx=-b/2a=2x*cosx/4 <==> 2Sinx=x*Cosx (**) Et par (*) et (**) on déduit que x²cos²x=4(2x-1) et Cos²x=2(1-x). Selon (*) 1/2<=x=<1 et on sait que x>=1/2 => x>1/5 <==> 4(2x-1)>2(x-1) alors x²Cos²x>Cos²x mais 1/2<=x=<1 => [cos²x]/4<=x²*cos²x=<cos²x Contradiction. On suppose maintenant que D>0 alors 0=<Sin²x<2x-1 donc x>=1/2 et selon A=x[x-Sin2x]=2Sin²x[x-1] (***)si x=<1 alors 1/2<=x=<Sin2x=<1 On retombe au premier cas. Maintenant si x>=1 on tire Sin2x=<1<x avec x=1 ne satisfait pas les données donc x différent de 1. Si x>1 alors 1-Sin2x<A=x^2 -xSin2x -2xSin²x +2Sin²x=0 donc Sin2x>1 Contradiction.. Donc S={0}. CQFD. J'ai déjà cité qu'on n'utilise pas le discriminent que si a, b et c ne dépendent pas de x. Pour te convaicre, je te donne un exemple: Soit l'équation: 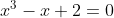 . Qui peut s'écrire autrement de la façon 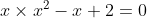 . Ce serait bête de continuer en utilisant le discriminent. Je suis désolé, mais ta solution me semble fausse. (  .) | |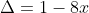
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Equation et trigonométrie: Mar 08 Mar 2011, 19:13 | |
| | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Equation et trigonométrie: Mar 08 Mar 2011, 21:13 | |
| @nmo : Normalement quand on veut utiliser Delta, on suppose que a,b et c sont constants, et cela sera vrai si Sin(x) ne dépend pas de x (Donne moi une formule si oui) . Les occasions dans lesquelles on a utilisé Delta pour vérifier si c'est vrai une fonction est surjective ne se comptent pas. . Merci pour l'information.
Je t'accorde qu'une méthode autre que celle du discriminent sera plus apprécié. | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Equation et trigonométrie: Mer 09 Mar 2011, 16:21 | |
| - nmo a écrit:
- Voici une équation, de ma création:
Résolvez en l'équation suivante .
Bonne chance. Je réponds en utilisant ma methode: En utilisant quelques formules trigonométriques, on trouve: }+2\sin^2{(x)}\big)+2\sin^2{(x)}=0&\Leftrightarrow x^2-x\big(\sin{(2x)}+1-\cos{(2x)}\big)+1-\cos{(2x)}=0\\&\Leftrightarrow 2x^2-2x\big(\sin{(2x)}+1-\cos{(2x)}\big)+2-2\cos{(2x)}=0\\&\Leftrightarrow 2x^2-2x\times \sin{(2x)}-2x\times(1-\cos{(2x)})+\sin^2{(2x)}+\cos^2{(2x)}+1-2\cos{(2x)}=0\\&\Leftrightarrow x^2-2x\times \sin{(2x)}+\sin^2{(2x)}+x^2-2x\times(1-\cos{(2x)})+(1-\cos{(2x)})^2=0\\&\Leftrightarrow \big(x-\sin{(2x)}\big)^2+\big(x-(1-\cos{(2x)})\big)^2=0\\&\Leftrightarrow \big(x-\sin{(2x)}\big)^2=0\text{ et }\big(x-(1-\cos{(2x)})\big)^2=0\\&\Leftrightarrow x-\sin{(2x)}=0\text{ et }x-(1-\cos{(2x)})=0\\&\Leftrightarrow x=\sin{(2x)}\text{ et }x=1-\cos{(2x)}\\&\Leftrightarrow x=\sin{(2x)}=1-\cos{(2x)}\end{align*}) . Et on a aussi: }=1-\cos{(2x)}&\Leftrightarrow \sin{(2x)}+\cos{(2x)}=1\\&\Leftrightarrow \frac{\sqrt{2}}{2}.\sin{(2x)}+\frac{\sqrt{2}}{2}.\cos{(2x)}=\frac{\sqrt{2}}{2}\\&\Leftrightarrow \cos{\frac{\pi}{4}}\cos{(2x)}+\sin{\frac{\pi}{4}}\sin{(2x)}=\cos{\frac{\pi}{4}}\\&\Leftrightarrow \cos{\big(\frac{\pi}{4}-2x\big)}=\cos{\frac{\pi}{4}}\\&\Leftrightarrow \frac{\pi}{4}-2x=\frac{\pi}{4}+2k\pi\text{ ou }\frac{\pi}{4}-2x=-\frac{\pi}{4}+2k'\pi\;\;;(k,k')\in\mathbb{Z}\\&\Leftrightarrow -2x=2k\pi\text{ ou }-2x=-\frac{\pi}{2}+2k'\pi\;\;;(k,k')\in\mathbb{Z}\\&\Leftrightarrow x=-k\pi\text{ ou }x=\frac{\pi}{4}+k'\pi\;\;;(k,k')\in\mathbb{Z}\end{align*}) . Or, 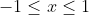 selon }=1-\cos{(2x)}) . Cela équivaut à dire que 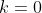 et 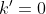 . Et par conséquent, 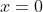 ou 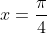 . Comme 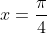n'est pas une solution, il vient que 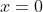. Donc 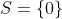 . Sauf erreur. | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Equation et trigonométrie: Mer 09 Mar 2011, 16:30 | |
| - M.Marjani a écrit:
- @nmo : Normalement quand on veut utiliser Delta, on suppose que a,b et c sont constants, et cela sera vrai si Sin(x) ne dépend pas de x (Donne moi une formule si oui) . Les occasions dans lesquelles on a utilisé Delta pour vérifier si c'est vrai une fonction est surjective ne se comptent pas. . Merci pour l'information.
Je t'accorde qu'une méthode autre que celle du discriminent sera plus apprécié. Selon le cercle trigonométrique, chaque x en radian a un sinus. On ne choisit plus de sinus arbitrairement. J'ai présenté une autre solution autre que celle de mizmaz, et j'attends des remarques. | |
|
| | |
derector
Habitué
Nombre de messages : 27
Age : 39
Date d'inscription : 04/03/2011
| | Sujet: Re: Equation et trigonométrie: Sam 23 Avr 2011, 21:58 | |
| and.it.webobo.biz
mercii je pense donc ,je suis | |
|
| | |
derector
Habitué
Nombre de messages : 27
Age : 39
Date d'inscription : 04/03/2011
| | Sujet: Re: Equation et trigonométrie: Sam 23 Avr 2011, 21:58 | |
| and.it.webobo.biz
mercii je pense donc ,je suis | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Equation et trigonométrie: | |
| |
|
| | |
| | Equation et trigonométrie: | |
|
