jacks
Habitué
 Nombre de messages : 27 Nombre de messages : 27
Age : 34
Date d'inscription : 25/04/2011
 |  Sujet: maximum value Sujet: maximum value  Mer 27 Avr 2011, 02:11 Mer 27 Avr 2011, 02:11 | |
| If  and  . then find Maximum value of  | |
|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: maximum value Sujet: Re: maximum value  Mer 27 Avr 2011, 19:03 Mer 27 Avr 2011, 19:03 | |
| - jacks a écrit:
- If
 and and  . then find Maximum value of . then find Maximum value of  Je vais répondre: On a d'un côté: }=\frac{\tan{B}+\tan{C}}{1-\tan{B}.\tan{C}}\\&\Leftrightarrow \frac{1}{\tan{A}}=\frac{\tan{B}+\tan{C}}{1-\tan{B}.\tan{C}}\\&\Leftrightarrow1-\tan{B}.\tan{C}=\tan{A}.(\tan{B}+\tan{C})\\&\Leftrightarrow\tan{A}.\tan{B}+\tan{B}.\tan{C}+\tan{C}.\tan{A}=1\end{align*}) . Et d'un autre côté, on a selon l'inégalité de Caushy schwartz: ^2&\le3\bigg((\sqrt{P})^2+(\sqrt{Q})^2+(\sqrt{R})^2\bigg)\\&=3(P+Q+R)\\&=3(5+\tan{A}.\tan{B}+5+\tan{B}.\tan{C}+5+\tan{C}.\tan{A})\\&=3\bigg(15+(\tan{A}.\tan{B}+\tan{B}.\tan{C}+\tan{C}.\tan{A})\bigg)\\&=3(15+1)\\&=3\times16\end{align*}) . Donc  . Il s'ensuit que la valeur maximale de  est 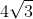 . Ce maximum est attent si et seulement si  . Donc  . Soit  . Et puisque les réels A, B, et C sont supérieurs à 0, alors  ,  , et  . Et par conséquent  . Et en vertu de  , il vient  . CQFD. Sauf erreur. | |
|
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: maximum value Sujet: Re: maximum value  Mer 27 Avr 2011, 21:06 Mer 27 Avr 2011, 21:06 | |
| | |
|
jacks
Habitué
 Nombre de messages : 27 Nombre de messages : 27
Age : 34
Date d'inscription : 25/04/2011
 |  Sujet: Re: maximum value Sujet: Re: maximum value  Sam 30 Avr 2011, 06:06 Sam 30 Avr 2011, 06:06 | |
| Thanks NMO for very Nice solution Using Cauchy-Schwartz Method. Now Here is My solution Using A.M >= G.M Inequality. =tan(\frac{\pi}{2}-C)\Leftrightarrow%20tanA.tanB+tanB.tanC+tanC.tanA=1}$\\\\%20Now%20$\mathbf{\left(\sqrt{P}+\sqrt{Q}+\sqrt{R}\right)^2=P+Q+R+2\sqrt{PQ}+2\sqrt{QR}+2\sqrt{RP}\leq%20P+Q+R+(P+Q)+(Q+R)+(R+P)}$\\\\%20So%20$\mathbf{\left(\sqrt{P}+\sqrt{Q}+\sqrt{R}\right)^2\leq%203.(P+Q+R)}$\\\\%20(Using%20$\mathbf{A.M\geq%20G.M}$)%20and%20Inequality%20hold%20When%20$\mathbf{P=Q=R}$\\\\%20$\mathbf{\Leftrightarrow%20\left(\sqrt{P}+\sqrt{Q}+\sqrt{R}\right)^2\leq%203.\left(5+tanA.tanB+5+tanB.tanC+5+tanC.tanA\right)\leq%203.(15+1)}$\\\\%20$\mathbf{\Leftrightarrow%20\left(\sqrt{P}+\sqrt{Q}+\sqrt{R}\right)\leq%204\sqrt{3}}$) | |
|
