Et pour la seconde somme, voici ce que j'ai fait:
Avant d'entammer l'exercice:
Soit n un entier naturel non nul.
On démontre premièrement, en utilisant une récurrence sur n, le résultat connu:
}=\frac{\sin{(n.x)}.\sin{\big((n+1).x\big)}}{\sin{(x)}})
.
On pose:
})
, et soit x un réél dont le sinus est non nul.
*On vérifie la propriété pour le plus petit indice n=1:
Puisque n=1, k varie de 1 jusqu'à 1 et par conséquent k=1.
Ainsi
})
.
Et comme
}.\sin{\big((1+1).x\big)}}{\sin{(x)}}=\frac{\sin{(x)}.\sin{(2x)}}{\sin{(x)}}=\sin{(2x)})
.
L'identité est bel et bien vraie au rang n=1.
*On démontre l'hérédité de la propriété:
Supposons que la propriété est vraie au rang n, et démontrons qu'elle l'est également au rang n+1.
On suppose que
}.\sin{\big((n+1).x\big)}}{\sin{(x)}})
, et on doit démontrer que
.x\big)}.\sin{\big((n+2).x\big)}}{\sin{(x)}})
. On a:
}\\&=\sum_{k=1}^{n}\sin{(2k.x)}+\sin{\big(2.(n+1).x\big)}\\&=\frac{\sin{(n.x)}.\sin{\big((n+1).x\big)}}{\sin{(x)}}+\sin{\big(2.(n+1).x\big)}\\&=\frac{\sin{(n.x)}.\sin{\big((n+1).x\big)}+\sin{\big(2.(n+1).x\big)}.\sin{(x)}}{\sin{(x)}}\\&=\frac{\sin{(n.x)}.\sin{\big((n+1).x\big)}+2.\sin{\big((n+1).x\big)}.\cos{\big((n+1).x\big)}.\sin{(x)}}{\sin{(x)}}\\&=\frac{\sin{\big((n+1).x\big)}.\bigg(\sin{(n.x)}+2.\cos{\big((n+1).x\big)}.\sin{(x)}\bigg)}{\sin{(x)}}\\&=\frac{\sin{\big((n+1).x\big)}.\bigg(\sin{(n.x)}+2.\sin{(x)}.\cos{(n.x+x)}\bigg)}{\sin{(x)}}\\&=\frac{\sin{\big((n+1).x\big)}.\bigg(\sin{(n.x)}+2.\sin{(x)}.\big(\cos{(n.x)}.\cos{(x)}-\sin{(n.x)}.\sin{(x)}\big)\bigg)}{\sin{(x)}}\\&=\frac{\sin{\big((n+1).x\big)}.\big(\sin{(n.x)}+2.\sin{(x)}.\cos{(n.x)}.\cos{(x)}-2.\sin{(x)}.\sin{(n.x)}.\sin{(x)}\big)}{\sin{(x)}}\end{align*})
.
Le latex ne peut pas supporter, on continue ici:
.x\big)}.\big(\sin{(n.x)}+2.\sin{(x)}.\cos{(n.x)}.\cos{(x)}-2.\sin{(x)}.\sin{(n.x)}.\sin{(x)}\big)}{\sin{(x)}}\\&=\frac{\sin{\big((n+1).x\big)}.\big(\sin{(n.x)}+\sin{(2x)}.\cos{(n.x)}-2.\sin^2{(x)}.\sin{(n.x)}\big)}{\sin{(x)}}\\&=\frac{\sin{\big((n+1).x\big)}.\big(\sin{(n.x)}.(1-2\sin^2{(x)})+\sin{(2x)}.\cos{(n.x)}\big)}{\sin{(x)}}\\&=\frac{\sin{\big((n+1).x\big)}.\big(\cos{(2x)}.\sin{(n.x)}+\sin{(2x)}.\cos{(n.x)}\big)}{\sin{(x)}}\\&=\frac{\sin{\big((n+1).x\big)}.\sin{(2x+n.x)}}{\sin{(x)}}\end{align*})
.
Soit
.x\big)}.\sin{\big((n+2).x\big)}}{\sin{(x)}})
.
*Conclusion de la récurrence:
(\forall x\in\mathbb{R}-\{k.\pi/k\in\mathbb{Z}\}):\sum_{k=1}^{n}\sin{(2k.x)}=\frac{\sin{(n.x)}.\sin{\big((n+1).x\big)}}{\sin{(x)}})
.
On passe maintenant à notre exercice:
On sait d'ores et déjà que
(\forall x\in\mathbb{R}-\{k.\pi/k\in\mathbb{Z}\}):\sum_{k=1}^{n-1}\sin{(2k.x)}=\frac{\sin{(n.x)}.\sin{\big((n-1).x\big)}}{\sin{(x)}})
.
On prends:
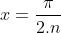
.
Il en résulte que:
:\sum_{k=1}^{n-1}\sin{(2k.\frac{\pi}{2.n})}=\frac{\sin{(n.\frac{\pi}{2.n})}.\sin{\big((n-1).\frac{\pi}{2.n}\big)}}{\sin{(\frac{\pi}{2.n})}})
.
Donc
:\sum_{k=1}^{n-1}\sin{(\frac{k.\pi}{n})}=\frac{\sin{(\frac{\pi}{2})}.\sin{(n.\frac{\pi}{2.n}-\frac{\pi}{2.n})}}{\sin{(\frac{\pi}{2.n})}})
.
Donc
:\sum_{k=1}^{n-1}\sin{(\frac{k.\pi}{n})}=\frac{1\times\sin{(\frac{\pi}{2}-\frac{\pi}{2.n})}}{\sin{(\frac{\pi}{2.n})}})
.
Donc
:\sum_{k=1}^{n-1}\sin{(\frac{k.\pi}{n})}=\frac{\cos{(\frac{\pi}{2.n})}}{\sin{(\frac{\pi}{2.n})}})
.
Donc
:\sum_{k=1}^{n-1}\sin{(\frac{k.\pi}{n})}=\frac{1}{\tan{(\frac{\pi}{2.n})}})
.
CQFD.
Sauf erreur.
