| | En attendant le début du jeu d'été |  |
|
|
| Auteur | Message |
|---|
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: En attendant le début du jeu d'été Sujet: En attendant le début du jeu d'été  Mar 14 Juin 2011, 17:55 Mar 14 Juin 2011, 17:55 | |
| En attendant le début du jeu d'été, je vous propose cette inégalité (de ma création  ) . Soient 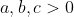 tel que 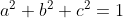 . Monterer que : ^4}\geq%20\frac{3}{2}) | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: En attendant le début du jeu d'été Sujet: Re: En attendant le début du jeu d'été  Mar 14 Juin 2011, 22:25 Mar 14 Juin 2011, 22:25 | |
| l'inégalité est équivalente à
(c/2ab)²+(a/2bc)²+(b/2ac)²>=3/2
on utilise IAG (c/2ab)²+(a/2bc)²+(b/2ac)² >=1/2(1/a² + 1/b² + 1/c²)
a,b,c>0 et a²+b²+c²=1 donc a<1 et b<1 et c<1
ce qui finit la démonstration | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: En attendant le début du jeu d'été Sujet: Re: En attendant le début du jeu d'été  Mar 14 Juin 2011, 22:55 Mar 14 Juin 2011, 22:55 | |
| pour la première équivalence c'est pas exacte car sigma et sous le racine carré | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: En attendant le début du jeu d'été Sujet: Re: En attendant le début du jeu d'été  Mar 14 Juin 2011, 23:03 Mar 14 Juin 2011, 23:03 | |
| oué j'avais fait une faute d’inattention >< | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: En attendant le début du jeu d'été Sujet: Re: En attendant le début du jeu d'été  Mar 14 Juin 2011, 23:34 Mar 14 Juin 2011, 23:34 | |
| ma démonstration se base sur l'inégalité suivante x²+y²+z²>=xy+yz+xz pr tous x,y,z de IR
rac[(c²/2a²b²)²+(a²/2b²c²)²+(b²/2a²c²)²]>=rac(1/4a^4 + 1/4b^4 + 1/4c^4)=1/2rac(1/a^4 + 1/b^4 + 1/c^4)>=1/2(1/(ab)² + 1/(ac)² + 1/(bc)²)>= 1/2(1/a²bc + 1/ab²c + 1/abc²)= 1/2abc (1/a + 1/b + 1/c)
a,b,c>0 et a²+b²+c²=1 donc a<1 et b<1 et c<1 d'ou 1/abc*( 1/a + 1/b + 1/c)>=3
ce qui finit la démonstration | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: En attendant le début du jeu d'été Sujet: Re: En attendant le début du jeu d'été  Mar 14 Juin 2011, 23:43 Mar 14 Juin 2011, 23:43 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 | |
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: En attendant le début du jeu d'été Sujet: Re: En attendant le début du jeu d'été  Mer 15 Juin 2011, 12:12 Mer 15 Juin 2011, 12:12 | |
| - boubou math a écrit:
- ma démonstration se base sur l'inégalité suivante x²+y²+z²>=xy+yz+xz pr tous x,y,z de IR
rac[(c²/2a²b²)²+(a²/2b²c²)²+(b²/2a²c²)²]>=rac(1/4a^4 + 1/4b^4 + 1/4c^4)=1/2rac(1/a^4 + 1/b^4 + 1/c^4)>=1/2(1/(ab)² + 1/(ac)² + 1/(bc)²)>= 1/2(1/a²bc + 1/ab²c + 1/abc²)= 1/2abc (1/a + 1/b + 1/c)
a,b,c>0 et a²+b²+c²=1 donc a<1 et b<1 et c<1 d'ou 1/abc*( 1/a + 1/b + 1/c)>=3
ce qui finit la démonstration Veuillez expliquer ce qui est en gras. En plus, tu n'es pas arrivé au résultat qu'on veut démontrer. | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: En attendant le début du jeu d'été Sujet: Re: En attendant le début du jeu d'été  Mer 15 Juin 2011, 12:15 Mer 15 Juin 2011, 12:15 | |
| Je suis en train de rédiger ma solution en latex! | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: En attendant le début du jeu d'été Sujet: Re: En attendant le début du jeu d'été  Mer 15 Juin 2011, 12:16 Mer 15 Juin 2011, 12:16 | |
| - Nayssi a écrit:
- Je suis en train de rédiger ma solution en latex!
OK. | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: En attendant le début du jeu d'été Sujet: Re: En attendant le début du jeu d'été  Mer 15 Juin 2011, 12:33 Mer 15 Juin 2011, 12:33 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: En attendant le début du jeu d'été Sujet: Re: En attendant le début du jeu d'été  Mer 15 Juin 2011, 12:39 Mer 15 Juin 2011, 12:39 | |
| | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 | |
  | |
yasmine
Maître

 Nombre de messages : 71 Nombre de messages : 71
Age : 29
Localisation : terrrrrrrre
Date d'inscription : 09/04/2011
 |  Sujet: Re: En attendant le début du jeu d'été Sujet: Re: En attendant le début du jeu d'été  Mer 15 Juin 2011, 17:44 Mer 15 Juin 2011, 17:44 | |
| bravo.mais j'ai encore un problème avec le sigma.que signifie 'cyc'? | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: En attendant le début du jeu d'été Sujet: Re: En attendant le début du jeu d'été  Mer 15 Juin 2011, 18:15 Mer 15 Juin 2011, 18:15 | |
| as-tu jeté un coup d’œil sur le livre des inégalités d'Animaths? | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: En attendant le début du jeu d'été Sujet: Re: En attendant le début du jeu d'été  | |
| |
|
  | |
| | En attendant le début du jeu d'été |  |
|
