| | exeo principes |  |
|
+5kaj mima yasserito nmo az360 ayoublekhl 9 participants |
| Auteur | Message |
|---|
ayoublekhl
Habitué
 Nombre de messages : 28 Nombre de messages : 28
Age : 29
Date d'inscription : 30/06/2011
 |  Sujet: exeo principes Sujet: exeo principes  Jeu 30 Juin 2011, 11:07 Jeu 30 Juin 2011, 11:07 | |
| on a
n un nombre entier naturel et n>=2
démontrer que n^4+4 n'est pas un nombre premier
(cet exercices m'a été posé dans un test pour passer au SM mais malheureusement j'ai eu 9.5/20 "déprimant non ?" et j'ai focus cet exo jusqu'à que j'ai parvenu à la réponse )
Tentez votre chance aussi | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 11:27 Jeu 30 Juin 2011, 11:27 | |
| n^4 + 4 = n^4 + 4n^2 +4 - 4n^2 = (n^2 + 2 - 2n)(n^2 + 2 + 2n) On a n>=2 => (n - 1)^2 + 1 > 1 d’où le résultat .  | |
|
  | |
ayoublekhl
Habitué
 Nombre de messages : 28 Nombre de messages : 28
Age : 29
Date d'inscription : 30/06/2011
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 11:44 Jeu 30 Juin 2011, 11:44 | |
| bonne réponse  tu peux me donner une question pour que je sache si je mérite le SM ou non ? Car ca m'intrigue la note que j'ai recu en test :/ | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 15:56 Jeu 30 Juin 2011, 15:56 | |
| Je te propose de faire cet exercice: Soit ABC un triangle, on note AB=c, BC=a, et CA=b. Dans ce triangle, on a:  et  . Calculez AB. Bonne chance. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 16:04 Jeu 30 Juin 2011, 16:04 | |
| on a (sin(A)+sin(B))/(a+b) = sin(C)/c= sin(C)/AB=7/6
alors AB=6/7 . sauf erreur | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 16:26 Jeu 30 Juin 2011, 16:26 | |
| - yasserito a écrit:
- on a (sin(A)+sin(B))/(a+b) = sin(C)/c= sin(C)/AB=7/6
alors AB=6/7 . sauf erreur Bien, ta solution est bonne. Ce que j'ai voulu estimer c'est sa maitrise de la loi des sinus et des caractéristiques de la proportionnalité. | |
|
  | |
ayoublekhl
Habitué
 Nombre de messages : 28 Nombre de messages : 28
Age : 29
Date d'inscription : 30/06/2011
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 16:38 Jeu 30 Juin 2011, 16:38 | |
| mais dans une lecon (le produit scalaire ) on a fait une propriété celle-ci :
sinC/c=sinA/b=sinB/b
mais je ne sais pas comment il a fait pour réunir les sinA et les SinB | |
|
  | |
ayoublekhl
Habitué
 Nombre de messages : 28 Nombre de messages : 28
Age : 29
Date d'inscription : 30/06/2011
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 16:42 Jeu 30 Juin 2011, 16:42 | |
| J'ai vu une fois une loi qui est comme ca :
a/b=c/d=a+c/b+d
mais je ne savais pas d'où elle venait donc je ne l'ai pas utilisé | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 17:01 Jeu 30 Juin 2011, 17:01 | |
| - ayoublekhl a écrit:
- J'ai vu une fois une loi qui est comme ca :
a/b=c/d=a+c/b+d
mais je ne savais pas d'où elle venait donc je ne l'ai pas utilisé 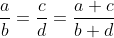 est vraie, et très utile. | |
|
  | |
ayoublekhl
Habitué
 Nombre de messages : 28 Nombre de messages : 28
Age : 29
Date d'inscription : 30/06/2011
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 17:12 Jeu 30 Juin 2011, 17:12 | |
| tu peux me dire comment on a démontré cette loi svp ? | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 17:12 Jeu 30 Juin 2011, 17:12 | |
| mais a condition que b=/= -d | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 17:14 Jeu 30 Juin 2011, 17:14 | |
| c'est facile : on a a/b=c/d alors ad=bc alors ad+ab=bc+ab ainsi a(b+d)=b(a+c)
alors a/b=(b+d)/(a+c)=c/d. sauf erreur . | |
|
  | |
ayoublekhl
Habitué
 Nombre de messages : 28 Nombre de messages : 28
Age : 29
Date d'inscription : 30/06/2011
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 17:21 Jeu 30 Juin 2011, 17:21 | |
| ah ok merci
Svp pour la filière SM les exos sont difficiles comme ce qu'on met dans les posts ? | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 17:29 Jeu 30 Juin 2011, 17:29 | |
| Par exemple ?  | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 17:33 Jeu 30 Juin 2011, 17:33 | |
| - Mehdi.O a écrit:
- Par exemple ?
  Pas à ce point je pense, puisqu'il y a ici beacoup d'exercices d'olympiades qui se déroulent, et qui n'ont rien à voir avec le programme des maths de première. Sache que la branche sciences mathématiques est une branche normale qui n'est pas très difficile, mais qui nécessite du travail, et de prendre les choses au sérieux... Ce n'est pas la peine de se faire peur,,, In my opinion, it gets really harder after Bac, not now  Am I wrong? | |
|
  | |
ayoublekhl
Habitué
 Nombre de messages : 28 Nombre de messages : 28
Age : 29
Date d'inscription : 30/06/2011
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 17:35 Jeu 30 Juin 2011, 17:35 | |
| par exemple les exos de IMMO ou les posts de geom :S le fait de ne pas pouvoir les résoudre me déprime  | |
|
  | |
ayoublekhl
Habitué
 Nombre de messages : 28 Nombre de messages : 28
Age : 29
Date d'inscription : 30/06/2011
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 17:43 Jeu 30 Juin 2011, 17:43 | |
| sinon faut être un génie pour passer aux SM ou bien résoudre ces posts ? :/ | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 17:48 Jeu 30 Juin 2011, 17:48 | |
|  , non c'est à force de travailler c'est tout. D'autant plus ces exercices ne figurent pas le problème de SM et ne sont pas d'une difficulté extra-ordinaire, bien au contraire il s'agit de petites astuces c'est tout  | |
|
  | |
ayoublekhl
Habitué
 Nombre de messages : 28 Nombre de messages : 28
Age : 29
Date d'inscription : 30/06/2011
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 18:04 Jeu 30 Juin 2011, 18:04 | |
| Merci beaucoup
Désolé si je fonce dans des détails banals mais je veux savoir comment un élève qui fait beaucoup d'exos devient plus fort .. sauf s'il apprend les solutions | |
|
  | |
steve 94
Féru

 Nombre de messages : 60 Nombre de messages : 60
Age : 31
Localisation : RABAT
Date d'inscription : 18/01/2011
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 18:09 Jeu 30 Juin 2011, 18:09 | |
| Je sais pourquoi t'a autant le traque , faut travailler régulièrement et avoir de l'envie ,c'est sur faut travailler mais bon pour la qualité et non pas pour la quantité!! | |
|
  | |
ayoublekhl
Habitué
 Nombre de messages : 28 Nombre de messages : 28
Age : 29
Date d'inscription : 30/06/2011
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Jeu 30 Juin 2011, 18:30 Jeu 30 Juin 2011, 18:30 | |
| Oui ce traque m'affaibli du coup quelques exos que j'ai déjà fais il y'a longtemps lorsque je les révise maintenant je les trouve comme des roches tout cela à cause d'un test de maths pour entrer à une lycée dans lequel j'ai eu 9.5 .. bref j'ai perdu ma confiance en soi et aussi je doute sur mon niveau de mathématiques sachant que pendant l'année je n'obtient que des bonnes notes  | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Dim 17 Mar 2013, 20:03 Dim 17 Mar 2013, 20:03 | |
| - ayoublekhl a écrit:
- on a
n un nombre entier naturel et n>=2
démontrer que n^4+4 n'est pas un nombre premier
(cet exercices m'a été posé dans un test pour passer au SM mais malheureusement j'ai eu 9.5/20 "déprimant non ?" et j'ai focus cet exo jusqu'à que j'ai parvenu à la réponse )
Tentez votre chance aussi generalement a^4+4b^4=(a^2+2b^2+2ab)(a^2+2b^2-2ab) | |
|
  | |
aminesm
Féru
 Nombre de messages : 60 Nombre de messages : 60
Age : 26
Localisation : rabat
Date d'inscription : 25/02/2014
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  Ven 28 Fév 2014, 00:07 Ven 28 Fév 2014, 00:07 | |
| pour l’exercice au debut est ce que c'est juste svp:
n^4+4=(n²)²+2²
=(n²+2)²-2xn²x2 parce que: a²+b²=(a+b)²-2ab
=(n²+2)²-4n²
=(n²+2)²-(2n)²
n^4+4=(n²+2+2n)(n²+2-2n) parce que a²-b²=(a+b)(a-b) | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: exeo principes Sujet: Re: exeo principes  | |
| |
|
  | |
| | exeo principes |  |
|
