| | Triangle équilatéral |  |
|
|
| Auteur | Message |
|---|
dhiab
Féru

 Nombre de messages : 56 Nombre de messages : 56
Age : 61
Date d'inscription : 27/01/2010
 |  Sujet: Triangle équilatéral Sujet: Triangle équilatéral  Sam 27 Aoû 2011, 10:44 Sam 27 Aoû 2011, 10:44 | |
| a , b , c sont les longeurs d'un triangle tel que ;  Montrez que cet triangle est équilatéral. | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Triangle équilatéral Sujet: Re: Triangle équilatéral  Sam 27 Aoû 2011, 13:26 Sam 27 Aoû 2011, 13:26 | |
| Solution :
on a : (a+b) = 2+c et 2ab = 4+c²
alors on a : (a+b)² >= 4ab <==> (2+c)² >= 8 + 2c² ce qui implique que c = 2 .
alors l'equation deviendra :
a+b = 4 et a*b = 4
ce qui implique aussé a = b = 2
donc le triangle équilatérale
Dernière édition par az360 le Sam 27 Aoû 2011, 19:52, édité 1 fois | |
|
  | |
geom
Maître
 Nombre de messages : 189 Nombre de messages : 189
Age : 30
Date d'inscription : 30/04/2011
 |  Sujet: Re: Triangle équilatéral Sujet: Re: Triangle équilatéral  Sam 27 Aoû 2011, 15:11 Sam 27 Aoû 2011, 15:11 | |
| - az360 a écrit:
- Solution :
on a : (a+b) = 2+c et 2ab = 4+c²
alors on a : (a+b)² >= 4ab <==> (2+c)² >= 8 + c² ce qui implique que c = 2 .
alors l'equation deviendra :
a+b = 4 et a*b = 4
ce qui implique aussé a = b = 2
donc le triangle équilatérale pourquoi? | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Triangle équilatéral Sujet: Re: Triangle équilatéral  Sam 27 Aoû 2011, 15:37 Sam 27 Aoû 2011, 15:37 | |
| - geom a écrit:
- az360 a écrit:
- Solution :
on a : (a+b) = 2+c et 2ab = 4+c²
alors on a : (a+b)² >= 4ab <==> (2+c)² >= 8 + c² ce qui implique que c = 2 .
alors l'equation deviendra :
a+b = 4 et a*b = 4
ce qui implique aussé a = b = 2
donc le triangle équilatérale pourquoi? on a : 2(a² + b²) >= (a+b)² et (a+b)²>=2(a²+b²) ==> 2a² + 2b² = a² + b² + 2ab <=> (a-b)² = 0 <=> a = b tu pose : a = c et b = 2  . | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Triangle équilatéral Sujet: Re: Triangle équilatéral  Sam 27 Aoû 2011, 18:01 Sam 27 Aoû 2011, 18:01 | |
| - az360 a écrit:
- Solution :
on a : (a+b) = 2+c et 2ab = 4+c²
alors on a : (a+b)² >= 4ab <==> (2+c)² >= 8 + c² ce qui implique que c = 2 .
alors l'equation deviendra :
a+b = 4 et a*b = 4
ce qui implique aussé a = b = 2
donc le triangle équilatérale Tu n'a pas bien tapis la coefessient de c² en rouge. Mais ce n'est pas une implication si tu considére celui-là seule sans ajouté autre. Autre Solution:(a+b)²=(c+2)² <=> a²+b²+(c²+4)=c²+4+4c <==> a²+b²=4c <==> (a-b)²=2(2c-ab)>=0 Donc 2c>=ab <=> 2*2c>=2ab=c²+4 <==> (c-2)²=<0 <=> c=2 Alors a+b=4 et ab=4 ==> a(4-a)=4 <=> a²-4a+4=0 <=> a=2 donc b=2.
Dernière édition par M.Marjani le Sam 27 Aoû 2011, 18:10, édité 1 fois | |
|
  | |
dhiab
Féru

 Nombre de messages : 56 Nombre de messages : 56
Age : 61
Date d'inscription : 27/01/2010
 |  Sujet: Re: Triangle équilatéral Sujet: Re: Triangle équilatéral  Sam 27 Aoû 2011, 18:08 Sam 27 Aoû 2011, 18:08 | |
| | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Triangle équilatéral Sujet: Re: Triangle équilatéral  Sam 27 Aoû 2011, 19:51 Sam 27 Aoû 2011, 19:51 | |
| OUiii merci marjani j'ai oublier un 2 a coté de c. edité  . | |
|
  | |
dhiab
Féru

 Nombre de messages : 56 Nombre de messages : 56
Age : 61
Date d'inscription : 27/01/2010
 |  Sujet: Re: Triangle équilatéral Sujet: Re: Triangle équilatéral  Dim 28 Aoû 2011, 08:53 Dim 28 Aoû 2011, 08:53 | |
| Salut a tous Récompense de votre aide voici une solution : Partant de : 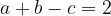 On obtient : ^{2}=4) On aura : 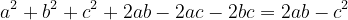 car : 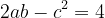 Donc: ^{2}+(b-c)^{2}=0) Conclusion a-c =0 et b-c= 0 Finalement a = b = c On remplaçant on obtient a = b = c = 2 Cordialement  | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Triangle équilatéral Sujet: Re: Triangle équilatéral  Dim 28 Aoû 2011, 13:05 Dim 28 Aoû 2011, 13:05 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Triangle équilatéral Sujet: Re: Triangle équilatéral  | |
| |
|
  | |
| | Triangle équilatéral |  |
|
