| | Equation fonctionnelle.. |  |
|
+5abdelbaki.attioui legend-crush killua 001 Chakibfovitsh achrafii 9 participants |
| Auteur | Message |
|---|
achrafii
Débutant
 Nombre de messages : 7 Nombre de messages : 7
Age : 29
Date d'inscription : 14/10/2011
 |  Sujet: Equation fonctionnelle.. Sujet: Equation fonctionnelle..  Ven 14 Oct 2011, 18:45 Ven 14 Oct 2011, 18:45 | |
| Salut ! quelque soit (x,y) appartient à IR trouvez tous les fonctions : f(xy)=f(x)f(y) Merci d'avance.  | |
|
  | |
Chakibfovitsh
Débutant
 Nombre de messages : 2 Nombre de messages : 2
Age : 28
Date d'inscription : 27/10/2012
 |  Sujet: Re: Equation fonctionnelle.. Sujet: Re: Equation fonctionnelle..  Sam 27 Oct 2012, 12:40 Sam 27 Oct 2012, 12:40 | |
| Salut  f(xy)=f(x)f(y) Supposons que x=y=0 <===> f(0)=f(0)² <===>f(0)=0 où f(0)=1 supposons que y=0 <===> f(0)=f(x)f(0) le cas où f(0)=0 0=0 c nul le cas où f(0)=1 f(x)*1=1 f(x)=1 ^^ Lahouma Zidné 3ilmaaaaaaaa | |
|
  | |
killua 001
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 29
Localisation : Ma chambre :D
Date d'inscription : 02/05/2012
 |  Sujet: Re: Equation fonctionnelle.. Sujet: Re: Equation fonctionnelle..  Sam 27 Oct 2012, 14:23 Sam 27 Oct 2012, 14:23 | |
| f(x)=x est solution ossi :/ | |
|
  | |
killua 001
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 29
Localisation : Ma chambre :D
Date d'inscription : 02/05/2012
 |  Sujet: Re: Equation fonctionnelle.. Sujet: Re: Equation fonctionnelle..  Sam 27 Oct 2012, 14:26 Sam 27 Oct 2012, 14:26 | |
| cette equation est tres classique dont les solutions sont : f(x)=x^a | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Equation fonctionnelle.. Sujet: Re: Equation fonctionnelle..  Dim 29 Déc 2013, 10:09 Dim 29 Déc 2013, 10:09 | |
| f(x)=0 est solution aussi sans etre sous la forme x^a ^^ | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: Equation fonctionnelle.. Sujet: Re: Equation fonctionnelle..  Dim 29 Déc 2013, 12:25 Dim 29 Déc 2013, 12:25 | |
| si f(a)=0 pour un a non nul ==> f(x)=f(a.x/a)=f(a)f(x/a)=0
==> f est l'application nulle ( c'est une solution)
supposons f non identiquement nulle
f(1)=f(1)² ===> f(1)=1
si x>0 ==> f(x)=f(Vx)²>0 . on pose alors g(x)= Ln(f(exp(x))) pour tout x dans R
g(x+y)=Ln(f(exp(x).exp(y)))=Ln(f(exp(x)).f(exp(y))) = Ln(f(exp(x)))+ Ln(f(exp(y)))=g(x)+g(y)
alors g vérifie l'équation de Cauchy
Avec une hypothèse ( par exemple g majorée sur un intervalle borné)
on sait que g(x)=µ.x
==> f(exp(x)) =exp(µ.x)
==> pour x>0, f(x)=x^µ
si x<0, f(x)f(-1)=f(-x)= (-x)^µ
mais f(-1)²=f(1)=1.
Donc qqs x dans R, f(x)=x^µ si x>=0 , f(-x)= c(-x)^µ si x<0 avec c²=1 et µ >=0
f(0)=0 par continuité | |
|
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: Equation fonctionnelle.. Sujet: Re: Equation fonctionnelle..  Dim 29 Déc 2013, 16:26 Dim 29 Déc 2013, 16:26 | |
| 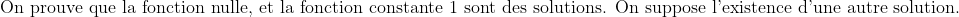 &space;=&space;f(x)^n&space;\Leftrightarrow&space;f&space;\textrm{&space;est&space;strictement&space;croissante.}) =&space;a.)  [ ,&space;on&space;viendra&space;sûrement&space;à&space;trouver&space;que&space;:&space;})  Alors là, j'explique. On posant des valeurs arbitraires pour n, l'on remarque que l'on a une valeur rapprochée de a plus précise. Plus n est grande, plus on s'approche du 2. C'par intuition que j'ai déduis la valeur de la limite, le calcul reste à faire. &space;=&space;2.&space;\textrm{&space;On&space;deduit&space;que&space;f(x)=x&space;Dans&space;}\mathbb{N}&space;\textrm{&space;(Je&space;vous&space;conduis&space;vers&space;un&space;exo&space;du&space;manuel&space;de&space;la&space;1ere&space;annee&space;sc.&space;Maths)}) Le passage aussi nécessite des explications. Entre x= 2^n et y =2^n+1, il y'a 2^n éléments, pareil pour a=f(2^n) et b=f(2^n+1), et puisque f est "strictement" croissante, on déduit que pour tout ces éléments compris entre x et y, se trouve une image comprise entre a et b. D'où f(x) = x. Par récurrence inverse, on étend la relation sur Z. En remarquant que x*1/x = 1, on étend la relation sur Q. Puisque Q est dense dans R\Q (cette notion reste à vérifier, mais je crois comprendre que l'unique passage entre Q et R, est un jeu de densité), on peut étendre la relation dans Q. La solution assez sérieuse à démontrer est celle-ci. f(x) = x pour tout x dans R. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 | |
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: Equation fonctionnelle.. Sujet: Re: Equation fonctionnelle..  Jeu 02 Jan 2014, 21:03 Jeu 02 Jan 2014, 21:03 | |
| Oui Oui, j'ai un peu accéléré, j'ai senti^^
On prend f(2) = a.
f(2) < f(3) < f(4) <=> a < f(3) < a² <=> a^n < f(3)^n < a^2n
De même: [(3^n-1)/2)] x a < f(3^n) = f(3)^n < [(3^n + 1)/2] x a
on en déduit une double inégalité!!
(ça peut être faux, m'je crois que c'la bonne méthode, f'in, reste à vérifier) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Equation fonctionnelle.. Sujet: Re: Equation fonctionnelle..  Jeu 02 Jan 2014, 21:23 Jeu 02 Jan 2014, 21:23 | |
| - Sketshup a écrit:
- Oui Oui, j'ai un peu accéléré, j'ai senti^^
On prend f(2) = a.
f(2) < f(3) < f(4) <=> a < f(3) < a² <=> a^n < f(3)^n < a^2n
De même: [(3^n-1)/2)] x a < f(3^n) = f(3)^n < [(3^n + 1)/2] x a
on en déduit une double inégalité!!
(ça peut être faux, m'je crois que c'la bonne méthode, f'in, reste à vérifier) Je ne trouve pas comment tu fais pour aboutir à ce qui est en rouge. Même en prenant n=1, ton inégalité devient a<f(3)<2a qu'on ne peut pas y arriver en s'appuyant sur ce qui précède! | |
|
  | |
aymas
Maître
 Nombre de messages : 168 Nombre de messages : 168
Age : 28
Localisation : tanger
Date d'inscription : 07/02/2012
 |  Sujet: Re: Equation fonctionnelle.. Sujet: Re: Equation fonctionnelle..  Sam 04 Jan 2014, 20:50 Sam 04 Jan 2014, 20:50 | |
| Il y a une infinite de solution : 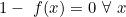 2- 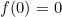 et 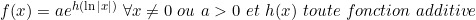 3- 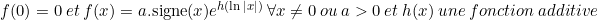
Dernière édition par aymas le Sam 04 Jan 2014, 22:16, édité 1 fois | |
|
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: Equation fonctionnelle.. Sujet: Re: Equation fonctionnelle..  Sam 04 Jan 2014, 21:15 Sam 04 Jan 2014, 21:15 | |
|  Un développement? | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Equation fonctionnelle.. Sujet: Re: Equation fonctionnelle..  Mer 05 Mar 2014, 19:45 Mer 05 Mar 2014, 19:45 | |
| je crois que
f(x)=0 et f(x)=1 pour tout x
f(x)=x^a pour tout x sont des solutions correctes...mais comment prouver la 2eme? ... | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Equation fonctionnelle.. Sujet: Re: Equation fonctionnelle..  | |
| |
|
  | |
| | Equation fonctionnelle.. |  |
|
