inégalié

Maître Nombre de messages : 279 Age : 27 Date d'inscription : 01/07/2011

a,b,c les longueurs des côtés d'un triangle et A son aire
prouver que a²+b²+c²>=4V3A
c'est un problème IMO mais pas difficile!
Bonne chance

$inégalié Gif.latex?\dpi{100}%20a^2+b^2+c^2-4\sqrt{3}A=2(b^2+c^2-2bc$
Sauf erreur...

Ou bien, si on pose: a=x+y et b=x+z et c=y+z (Transformation de Ravi), et p=∑x et q=∑xy et r=xyz, on trouve: $inégalié Gif$ (on applique la formule de Héron pour calculer la surface).
Et on a: 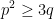$inégalié Gif$ donc: 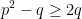$inégalié Gif$ , et : 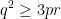$inégalié Gif$ , donc: 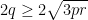$inégalié Gif$ , d'où: $inégalié Gif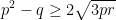$ , d'où le résultat voulut...

Maître Nombre de messages : 279 Age : 27 Date d'inscription : 01/07/2011

ali-mes a écrit:: $inégalié Gif.latex?\dpi{100}%20a^2+b^2+c^2-4\sqrt{3}A=2(b^2+c^2-2bc$
Sauf erreur...

Combien de ligne tu as sauté(loi des sinus,loi des cosinus...)?!!
Certes, on peut résoudre cet exercice en utilisant plusieurs méthodes. Je trouve que "loi des sinus + jensen" est la meilleure.
généralisation:

$inégalié Gif$

diablo902 a écrit:: généralisation:
$inégalié Gif$

En utilisant la substition de Ravi (avec a=x+y, b=y+z et c=z+x), l'inégalité à démontrer devient $inégalié Gif$ .
Ou encore $inégalié Gif$ .
Ainsi $inégalié Gif$ .
Ce qui est vrai, en posant 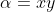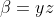$inégalié Gif$ , $inégalié Gif$ et 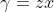$inégalié Gif$ (car on retrouve la fameuse inégalité $inégalié Gif.latex?(\sum_{cyc}\alpha)^2\ge3\sum_{cyc}\alpha$ , démontrable sans peine).
CQFD.
Sauf erreur.

Maître Nombre de messages : 279 Age : 27 Date d'inscription : 01/07/2011

Exact nmo
une autre méthode:
d'après la loi des cosinus : a²=b²+c²-2bc.cosA=(b-c)²+4A.tan(A/2)
[img]http://latex.codecogs.com/gif.latex?\small&space;a^2+b^2+c^2=\sum(a-b)^2+4A.\sum&space;tan(A/2) [img]
la fonction tan est convexe (on a A/2,B/2,C/2)
d'après jensen [img]http://latex.codecogs.com/gif.latex?\small&space;\sum&space;tan(A/2)\geq&space;3tan[(A+B+C)/3]=\sqrt&space;{3} [/img]
D'où le résultat Smile