| | younesmath2012---9 |  |
|
|
| Auteur | Message |
|---|
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: younesmath2012---9 Sujet: younesmath2012---9  Mer 08 Aoû 2012, 23:36 Mer 08 Aoû 2012, 23:36 | |
| | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Mer 08 Aoû 2012, 23:42 Mer 08 Aoû 2012, 23:42 | |
| WOOW, vous avez beaucoup d'inégalité MR.Younes a la fois  | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Mer 08 Aoû 2012, 23:53 Mer 08 Aoû 2012, 23:53 | |
| les inegalites ne finissent jamais Mr''oty'' | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Mer 08 Aoû 2012, 23:59 Mer 08 Aoû 2012, 23:59 | |
| oui vous avez raison comme toute chose en maths  | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 | |
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Jeu 09 Aoû 2012, 03:07 Jeu 09 Aoû 2012, 03:07 | |
| Vraiment tres belle inégalité voici Ma solution : posant x=a-b , y=b-c , z=c-a on a : x+y+z=0 l'inégalité est équivalente : (\frac{1}{x^{2}}+\frac{1}{y^2}+\frac{1}{z^{2}})&space;\geq{\frac{27}{2}}) , puisque l'inégalité reste homogène : Posant S=x+y+z=0 et Q=xy+yz+zx et P=xyz , par l’homogénéité on peut assumé : Q= -1 . alors l'inégalité est équivalente a : \geq{\frac{27}{2}}\Leftrightarrow&space;P^{2}\leq{\frac{27}{4}}&space;.) , puisque parmi les trois nombres x,y,z il existe tjrs 2 avec le même signe assumant xy >=0 on d'apres S=0 que z=-(x+y) , et d'apres Q= - 1 on en déduit que : (x+y)²=xy+1 . ainsi on posant t=xy . on a : ^{2}=t^2(t+1)=t^{3}+t^{2}) aussi on a d'apres xy+1=(x+y)² >=4xy que t=< 1\3 . et puisque :  (3t+2)^{2}&space;\leq{0}) ce qui est vrai , l'inégalité est démontré (sauf erreur ) . | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Jeu 09 Aoû 2012, 11:24 Jeu 09 Aoû 2012, 11:24 | |
| Est ce qu'on peut supposer que xy+xz+yz=-1 , étant donné qu'on a déjà la contrainte x+y+z=0 ? | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Jeu 09 Aoû 2012, 16:17 Jeu 09 Aoû 2012, 16:17 | |
| x²+y²+z²=(x+y+z)² - 2(xy+yz+xz)=-2(xy+yz+xz) donc le xy+yz+xz < 0 | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Jeu 09 Aoû 2012, 22:11 Jeu 09 Aoû 2012, 22:11 | |
| - Oty a écrit:
- x²+y²+z²=(x+y+z)² - 2(xy+yz+xz)=-2(xy+yz+xz) donc le xy+yz+xz < 0
je veux dire que tu ne peux pas supposer une autre contrainte sur les variables alors que tu as déjà une, même si l'expression est homogène.. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Jeu 09 Aoû 2012, 22:13 Jeu 09 Aoû 2012, 22:13 | |
| pk ? as tu un contre exemple ou tu peux le démontrer ? la premiere contrainte n'est pas du a l'homogénisation mais a la substitution | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Jeu 09 Aoû 2012, 23:40 Jeu 09 Aoû 2012, 23:40 | |
| pour voir que c'est possible , xy+yz+xz=-k² on remplace x=ka , y=kb ,z=kb ,alors : ab+bc+ca= - 1 et ka+kb+kc=0=> a+b+c=0 et ab+ac+bc=-1 ce systeme a plusieurs solution et puisque les ''k '' se simplifie on peut garder la notation x y et z , aussi ce raisonnement n'as marché que pour ce cas , sa ne veut pas dire qu'on peut le faire tout le temps dans le cas ou x+y+z=k ! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Ven 10 Aoû 2012, 00:27 Ven 10 Aoû 2012, 00:27 | |
| - Oty a écrit:
- Vraiment tres belle inégalité voici Ma solution : posant x=a-b , y=b-c , z=c-a on a : x+y+z=0 l'inégalité est équivalente :
(\frac{1}{x^{2}}+\frac{1}{y^2}+\frac{1}{z^{2}})&space;\geq{\frac{27}{2}}) , puisque l'inégalité reste homogène : Posant S=x+y+z=0 et Q=xy+yz+zx et P=xyz , par l’homogénéité on peut assumé : Q= -1 . alors l'inégalité est équivalente a : , puisque l'inégalité reste homogène : Posant S=x+y+z=0 et Q=xy+yz+zx et P=xyz , par l’homogénéité on peut assumé : Q= -1 . alors l'inégalité est équivalente a :
\geq{\frac{27}{2}}\Leftrightarrow&space;P^{2}\leq{\frac{27}{4}}&space;.) , puisque parmi les trois nombres x,y,z il existe tjrs 2 avec le même signe assumant xy >=0 on d'apres S=0 que z=-(x+y) , et d'apres Q= - 1 on en déduit que : (x+y)²=xy+1 . ainsi on posant t=xy . on a : , puisque parmi les trois nombres x,y,z il existe tjrs 2 avec le même signe assumant xy >=0 on d'apres S=0 que z=-(x+y) , et d'apres Q= - 1 on en déduit que : (x+y)²=xy+1 . ainsi on posant t=xy . on a :
^{2}=t^2(t+1)=t^{3}+t^{2}) aussi on a d'apres xy+1=(x+y)² >=4xy que t=< 1\3 . aussi on a d'apres xy+1=(x+y)² >=4xy que t=< 1\3 .
et puisque :

(3t+2)^{2}&space;\leq{0})
ce qui est vrai , l'inégalité est démontré (sauf erreur ) . Ou est le cas d'égalité? - ali-mes a écrit:
- Oty a écrit:
- x²+y²+z²=(x+y+z)² - 2(xy+yz+xz)=-2(xy+yz+xz) donc le xy+yz+xz < 0
je veux dire que tu ne peux pas supposer une autre contrainte sur les variables alors que tu as déjà une, même si l'expression est homogène.. Mois aussi; je pense qu'il n'a pas le droit de supposer une autre contrainte. Je crois qu'en ajoutant cette contrainte, on va diminuer les cas d'égalité; voire oublier quelques uns. Je présente ma solution dans quelques instants. Et j'attends des justifications qui tiennent au bout de la part de Oty s'il est encore sûr qu'on peut ajouter une nouvelle contrainte. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Ven 10 Aoû 2012, 00:42 Ven 10 Aoû 2012, 00:42 | |
| - younesmath2012 a écrit:
- Soient a,b et c des réels 2 à 2 distincts.
Montrez que: \bigg(\frac{1}{(a-b)^{2}}+\frac{1}{(b-c)^{2}}+\frac{1}{(c-a)^{2}}\bigg)\geq\frac{27}{4}) Comme la solution qui me précède, je mets 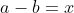 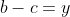 et 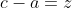 . On aura de plus que 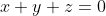 , et on doit démontrer que \bigg(\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{1}{z^{2}}\bigg)\geq\frac{27}{2}) . Selon le signe des nouvelles variables, on doit forcément avoir deux du même signe et un troisième qui est leur différent. Dans les deux cas à traiter, on se ramène à démontrer que \bigg(\frac{1}{\alpha^{2}}+\frac{1}{\beta^{2}}+\frac{1}{\gamma^{2}}\bigg)\geq\frac{27}{2}) où  ,  et 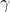 sont des réels positifs vérifiant  . En simplifions l'écriture, la dernière inégalité équivaut à ^2}+\frac{(\alpha+\beta)^2.(\alpha^2+\beta^2)}{(\alpha.\beta)^2}+\frac{\alpha^2+\beta^2}{(\alpha+\beta)^2}\ge\frac{21}{2}) . Ce qui est clairement vrai, en utilisant la fameuse inégalité de Cauchy Schwartz... (En effet, la première fraction est supérieure à 2, la seconde à 8 et la troisième à 1/2). Pour ce qui est du cas d'égalité; c'est quand deux variables sont égaux et le troisième et l'inverse de leurs somme. Ce qui se projette sur le problème initial par la fait que la somme de deux variables est le double du troisième. (C'est à dire si a+b=2c ou b+c=2a ou c+a=2b). CQFD. Sauf erreurs. | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Ven 10 Aoû 2012, 00:50 Ven 10 Aoû 2012, 00:50 | |
| | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Ven 10 Aoû 2012, 01:09 Ven 10 Aoû 2012, 01:09 | |
| @nmo , l'contrainte x+y+z=0 n'est pas du a l'homogénito mais au changement de variable ! le cas d'égalité est quand t=1\3 => x=y et z=-2c comme celui que tu as trouvé ! et aussi quand t=-2\3 . s'il vous plait ne réfuté pas une solution sans justification .
Dernière édition par Oty le Ven 10 Aoû 2012, 01:13, édité 1 fois | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Ven 10 Aoû 2012, 01:11 Ven 10 Aoû 2012, 01:11 | |
| - Oty a écrit:
- pour voir que c'est possible , xy+yz+xz=-k² on remplace x=ka , y=kb ,z=kb ,alors : ab+bc+ca= - 1 et ka+kb+kc=0=> a+b+c=0 et ab+ac+bc=-1 ce systeme a plusieurs solution et puisque les ''k '' se simplifie on peut garder la notation x y et z , aussi ce raisonnement n'as marché que pour ce cas , sa ne veut pas dire qu'on peut le faire tout le temps dans le cas ou x+y+z=k !
| |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Ven 10 Aoû 2012, 01:25 Ven 10 Aoû 2012, 01:25 | |
| Bon voila je vais clarifier encore : remarquon d''abord avant de faire la substition que :
[img]http://latex.codecogs.com/gif.latex?(a-b)(b-c)+(c-a)(b-c)+(a-b)(c-a)=-[\frac{3(b-c)^2+(2a-b-c)^2}{4}]<&space;0\Leftrightarrow&space;\exists&space;k^2&space;\{(a-b)(b-c)+(c-a)(b-c)+(a-b)(c-a)=-k^2\}[/img] on homogénisant avec a=km , b=kn , c=ks on a \sum (m-n)(n-s) = - 1 , on posant x=m-n , y=n-s ....
on a bien xy+yz+xz=-1 et x+y+z=0 . c'est le mieux que je puisse faire si vous n'etes pas tjrs convaincu j'abondonne .... | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Ven 10 Aoû 2012, 07:10 Ven 10 Aoû 2012, 07:10 | |
| Ma solution viens d'etre confirmé ICI | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Sam 11 Aoû 2012, 18:02 Sam 11 Aoû 2012, 18:02 | |
| salam wach ta9dar tjawab 3lih bla directe bla madjid chi contrainte!!!! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  Mar 14 Aoû 2012, 10:32 Mar 14 Aoû 2012, 10:32 | |
| - Oty a écrit:
- @nmo , l'contrainte x+y+z=0 n'est pas du a l'homogénito mais au changement de variable ! le cas d'égalité est quand t=1\3 => x=y et z=-2c comme celui que tu as trouvé ! et aussi quand t=-2\3 . s'il vous plait ne réfuté pas une solution sans justification .
- Oty a écrit:
- Ma solution viens d'etre confirmé ICI
Ce que je comprends de ce qui précède est la philosophie suivante: Si on part de la contrainte x+y+z=0, on peut écrire z=-(x+y) et démontrer l'inégalité seulement pour ces deux variables. Dans ce cas, l'inégalité est homogène; on peut donc supposer une contrainte sur x et y du type xy+x²+y²=1. En utilisant z=-(x+y), on doit avoir xy+yz+zx=-1. Je pense maintenant que l'affaire est claire. Je m'excuse pour ma hâte... | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: younesmath2012---9 Sujet: Re: younesmath2012---9  | |
| |
|
  | |
| | younesmath2012---9 |  |
|
