Problème1:Let
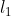
be the line which connects the tangency points other than in side
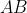
of the excircle of convex quadrilateral
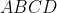
.
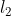
,

and

are similarly determined by the excircles of
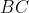
,
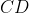
and

respectively.
Let

,

,

and

.
Prove that the line
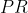
goes through the midpoint of
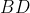
.
Problème2:Let x, y and z be positive real numbers such that

.
Prove that:
^2}\ge \frac{3}{(xy+yz+zx)^2})
.
Problème3:From three real number
)
we can get another three numbers either
)
or
)
.
Can we get
)
from
)
appliying these two operations adequately many times.
Problème4:Let
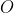
be the circumcenter of triangle
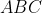
.
A line perpendicular to
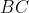
trough
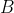
meets the midperpendicular
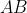
at
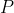
, and a line perpendicular to
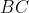
trough
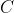
meets the midperpendicular
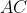
at
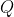
.
If
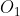
is the circumcenter of

, prove that

.
Problème5:Find all functions
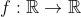
such that for any
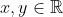
, the equality
+f(y)\big)=2x+f(y))
.
Problème6:Prove that for any

there exists
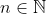
such that
)
.
Bonne chance.[b]
