Inégalité

Soit n>=2 un entier et a{1},a{2},a{3},............a{n} des réels tels que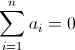
Inégalité Codeco10

Prouvez que
Inégalité Codeco11

c'est problème est faux , pour n=3 , a1=3 , a2=-2 , a3=-1
2(|3+2|+|-2+1|)-3(1+2+3)=12-18= - 6 < 0 !

Oty a écrit:: c'est problème est faux , pour n=3 , a1=3 , a2=-2 , a3=-1
2(|3+2|+|-2+1|)-3(1+2+3)=12-18= - 6 < 0 !

Tu as oublié |a_1-a_3|..

la somme develllopé ce n(est pas :
|a_{1}-a_{2}|+|a_{2}-a_[3}|+|a_{3}-a_{4}|+...+|a_{n-1}-a_{n}|
?

si c'est le cas alors je n'ai oublier que |a_[3}|=1 dans mons exemple ca reste encore négatif
nn ?

Oty a écrit:: la somme develllopé ce n(est pas :
|a_{1}-a_{2}|+|a_{2}-a_[3}|+|a_{3}-a_{4}|+...+|a_{n-1}-a_{n}|
?

Je crois que c'est plutôt: $Inégalité 9ac7d99373cb8a7f7da18b1ea03b7886f1ff5899$ . Il y a (n-1)+(n-2)+...+1=n(n-1)/2 termes. (pour chaque 2 indices tel que i<j)

Oty a écrit:: si c'est le cas alors je n'ai oublier que |a_[3}|=1 dans mons exemple ca reste encore négatif
nn ?

Bon , avec n=3,a1=3 , a2=-2 et a3=-1 , ça devient:

2(LHS-RHS)=2(|a_1-a_2|+|a_1-a_3|+|a_2-a_3|)-3(|a_1|+|a_2|+|a_3|)=2(5+4+1)-3(3+2+1)=2>0.

Merci Ali , je connaissais pas cette notation de sigma je croyais qu'elle désigné i et j consécutif ...

Cette notation du sigma est ce que Ali-mes a expliqué , mais vous n'avez tout de même pas encore donné une solution à cet exo Exclamation

pour l'instant j'ai fait un commencement mais je suis bloqué sur un point Neutral

....

lol finalement sa s'est débloquer cette inégalité n'est pas difficile avec l'explication de Ali ,
voici ma solution :
par l'inégalité triangulaire on a :
$Inégalité Gif.latex?|a_{1}-a_{2}|+|a_{1}-a_{3}|+...+|a_{1}-a_{n}|\geq&space;|(n-1)a_{1}-(a_{2}+a_{3}+..$
des inégalités similaire sont obtenue en changent a1 en a2 ainsi de suit .... puis en sommant toute c'est inegalité en obtient le resultat voulu .

je crois que c'est pas juste Oty puisque a_1 et a_2 ne jouent pas un role symetrique dans cette expression et d'en plus au de a_2 ;le nombre a_1 n'existe pas dans aucune valeur absolue puisque il existe juste n-2 termes dont a_1 n'est pas mentionne

je vais détaillé un peu plus pour toi Aymas .
en faite on utilise le simple fait que |-x|=|x| voici les lignes suivante :
$Inégalité Gif.latex?|a_{2}-a_{1}|+|a_{2}-a_{3}|+|a_{2}-a_{4}|+...+|a_{2}-a_{n}|\geq&space;|(n-1)a_{2}-(a_{1}+a_{3}+a_{4}+..$
puis encore :
$Inégalité Gif.latex?|a_{3}-a_{1}|+|a_{3}-a_{2}|+|a_{3}-a_{4}|+...+|a_{3}-a_{n}|\geq&space;|(n-1)a_{3}-(a_{1}+a_{2}+a_{4}+..$
en continue d'une manière analogue ...... jusqu'a :
$Inégalité Gif.latex?|a_{n}-a_{1}|+|a_{n}-a_{2}|+|a_{n}-a_{3}|+...+|a_{n}-a_{n-1}|\geq&space;|(n-1)a_{n}-(a_{1}+a_{2}+a_{3}+..$
on sommant toute s'est inégalité on a bien le membre de gauche :
$Inégalité Gif.latex?LHS=2(|a_{1}-a_{2}|+|a_{1}-a_{3}|+..+|a_{1}-a_{n}|)+2(|a_{2}-a_{3}|+|a_{2}-a_{4}|+...+|a_{2}-a_{n}|)+2(....$
le resultat en découle vue que le membre de droite est ''n \sum |ai|'' Smile

.

Habitué Nombre de messages : 25 Age : 28 Date d'inscription : 25/08/2012

ouais c 100 pourcent correct Smile

» inégalité
» inegalité
» inégalité
» InEGaLiTe
» Inégalité