encore-simple-fesable

younesmath2012 a écrit:: $encore-simple-fesable Gif.latex?a,b,c...%20\epsilon%20...\mathbb{R}...tq...a-b\neq%200...\neq%20et...b+c\neq%200...\neq%20et...c+a\neq%200 et...(a+c)(b+c)=1....MQ..$

Je propose ma solution:
On a premièrement: $encore-simple-fesable Gif$ ==>(*) (en s'appuyant sur la contrainte $encore-simple-fesable Gif$ ).
De plus, on a pour la même raison $encore-simple-fesable Gif$ .
L'inégalité est équivalente à $encore-simple-fesable Gif$ .
Il s'agit donc de l'inégalité arithmético-géométrique; La preuve prend fin.
Mais pour l'appliquer, il faut s'assurer que $encore-simple-fesable Gif$ est positif.
Cela est notre cas, en appliquent l'inégalité déjà annoncée.
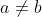
Le cas d'égalité n'existe pas car $encore-simple-fesable Gif$ selon l'hypothèse.
On écrit plus précisément $encore-simple-fesable Gif$ .
CQFD.
Sauf erreurs.

oui ,bravo ,c'est juste

younesmath2012 a écrit:: est ce qu'on a le droit d'ajouter la contrainte (a+c)(b+c)=1 a la condition (a+b)(b+c)(c+a)=1?????

Mr Younes vous avez ecris dans la contrainte (a+c)(b+c)=1 Smile

.

Oty a écrit:

younesmath2012 a écrit:: est ce qu'on a le droit d'ajouter la contrainte (a+c)(b+c)=1 a la condition (a+b)(b+c)(c+a)=1?????

Mr Younes vous avez ecris dans la contrainte (a+c)(b+c)=1 Smile

.

oui je l'ai edite ishabe li l'exercice ou j'ai posé (a+b)(b+c)(c+a)=8
merci!!!