| | exo-kitabe madrassi-tc |  |
|
|
| Auteur | Message |
|---|
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: exo-kitabe madrassi-tc Sujet: exo-kitabe madrassi-tc  Lun 27 Aoû 2012, 19:14 Lun 27 Aoû 2012, 19:14 | |
| x,y deux reels verifiant : 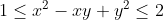 1)montrer que : 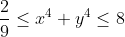 2)montrer que pour tout entier n>=2 on a : 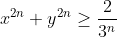
Dernière édition par younesmath2012 le Mar 28 Aoû 2012, 00:18, édité 1 fois | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Lun 27 Aoû 2012, 20:25 Lun 27 Aoû 2012, 20:25 | |
| Ma solution pour (1) membre de droite : ^2-2x^2y^2&space;\leq&space;(2+xy)^2-2x^2y^2=&space;4+4xy-x^2y^2) et ^2&space;\geq{0}) | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Lun 27 Aoû 2012, 21:20 Lun 27 Aoû 2012, 21:20 | |
| Ma solution pour (1) le membre de gauche : il suffit de prouver que : -2(x^2-xy+y^2)^2=7&space;x^4+4&space;x^3&space;y-6&space;x^2&space;y^2+4&space;x&space;y^3+7&space;y^4&space;\geq&space;0) ^2(7t^2-10t+7)\geq{0}) ce qui est vrai ou t=x\y  .
Dernière édition par Oty le Mar 28 Aoû 2012, 00:20, édité 1 fois | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Lun 27 Aoû 2012, 21:22 Lun 27 Aoû 2012, 21:22 | |
| Pour la 2) récurrence + chebichev en 3 ligne  . | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Lun 27 Aoû 2012, 23:44 Lun 27 Aoû 2012, 23:44 | |
| | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Lun 27 Aoû 2012, 23:57 Lun 27 Aoû 2012, 23:57 | |
| | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Mar 28 Aoû 2012, 00:03 Mar 28 Aoû 2012, 00:03 | |
| mnine jebti 9(x²+y²)-2(x²-xy+y²)² ???
hadchi liktebti mawadahch!!! | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Mar 28 Aoû 2012, 00:07 Mar 28 Aoû 2012, 00:07 | |
| - younesmath2012 a écrit:
- mnine jebti 9(x²+y²)-2(x²-xy+y²)² ???
hadchi liktebti mawadahch!!! Mr Younes rahe wade7 bezzaf ga3e sma7e lia car puisque andna x²-xy+y² >=1 on au lieu de prouvé que : 9(x^4+y^4)>=2 , on prouve cette inégalité ; 9(x^4+y^4)>=2(x²-xy+y²)>=2  . | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Mar 28 Aoû 2012, 00:15 Mar 28 Aoû 2012, 00:15 | |
| non mawadehch hit dakchi liktebti flawal faux ktebti -2(x^2-xy+y^2)^2=7&space;x^4+4&space;x^3&space;y-6&space;x^2&space;y^2+4&space;x&space;y^3+7&space;y^4&space;\geq&space;0) au lieu de x^4+y^4 ktebti x²+y² qui est fausse!!! mais daba bane ljawab diyalek!!! | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Mar 28 Aoû 2012, 00:20 Mar 28 Aoû 2012, 00:20 | |
| Ah je viens de le remarquer désolé . Merci beaucoup , c'est édité .
| |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Mar 28 Aoû 2012, 00:24 Mar 28 Aoû 2012, 00:24 | |
| - Oty a écrit:
- Pour la 2) récurrence + chebichev en 3 ligne
 . . comment tu va demarer pour utilser ''chebichev'' tu n'as pas x²+y²>=2/3 ??????? | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Mar 28 Aoû 2012, 00:39 Mar 28 Aoû 2012, 00:39 | |
| puisque n=2 c'est vrai , pour n> 2 alors n=p+2 :)avec p>=1 . , en effectue une récurrence forte sur p . ou bien on utilise Power-mean AM-GM , on revient au cas ou n=2  . | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Mar 28 Aoû 2012, 01:06 Mar 28 Aoû 2012, 01:06 | |
| hawal tjaweb 3liha bla reccurence
je vous laisse 3jours pour reflechir a la 2eme question!!! | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Mar 28 Aoû 2012, 01:39 Mar 28 Aoû 2012, 01:39 | |
| avec vous il faut tout détaillé  , pas besoin de récurrance juste AM-GM . [img]http://latex.codecogs.com/gif.latex?\sqrt[2n]{\frac{x^{2n}+y^{2n}}{2}}&space;\geq&space;\sqrt[4]{\frac{x^4+y^{4}}{2}}=>x^{2n}+y^{2n}\geq&space;2&space;(\sqrt[4]{\frac{x^4+y^{4}}{2}})^{2n}\geq&space;\frac{2}{3^{n}}[/img]
Dernière édition par Oty le Mar 28 Aoû 2012, 01:47, édité 1 fois | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Mar 28 Aoû 2012, 01:44 Mar 28 Aoû 2012, 01:44 | |
| c'est juste tbarkellah 3lik!!! | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  Mar 28 Aoû 2012, 01:46 Mar 28 Aoû 2012, 01:46 | |
| pour la récurrence n>=2 puisque pour n=2 l'inégalité est deja prouver , assumant n=p+2 avec p=0 l'inégalité , assumant l'inégalité vrai pour p>=1 et pour (p-1) (récurrence forte ) et montrons l"inégalité pour p+1 , c'est a dire que : +2)})&space;+&space;y^4(y^{2((p-1)+2)})\geq&space;\frac{(x^4+y^4)(x^{2((p-1)+2)}+y^{2((p-1)+2)})}{2}&space;\geq&space;\frac{2}{3^{p+3}}) (chebisev pour x >=y ) | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: exo-kitabe madrassi-tc Sujet: Re: exo-kitabe madrassi-tc  | |
| |
|
  | |
| | exo-kitabe madrassi-tc |  |
|
