| | x+y+z=1/x+1/y+1/z |  |
|
|
| Auteur | Message |
|---|
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: x+y+z=1/x+1/y+1/z Sujet: x+y+z=1/x+1/y+1/z  Mer 29 Aoû 2012, 01:33 Mer 29 Aoû 2012, 01:33 | |
| x,y,z >0 tq 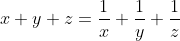 montrer que : 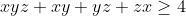 | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: x+y+z=1/x+1/y+1/z Sujet: Re: x+y+z=1/x+1/y+1/z  Mer 29 Aoû 2012, 11:16 Mer 29 Aoû 2012, 11:16 | |
| Bonjour, voici ce que j'ai fait: Premièrement , on fait la substitution: 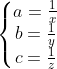 , la condition devient: =ab+ac+bc) . Et l'inégalité à démontrer est: 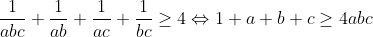 . On pose: p=a+b+c, q=ab+ac+bc et r=abc. Il vient qu'on a: pr=q, et on veut démontrer que: 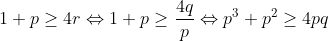 . D'après Schur: 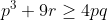 , donc il suffit montrer que: 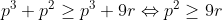 . ce qui est vrai, car on a: 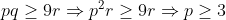 . d'où: 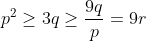 ... | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: x+y+z=1/x+1/y+1/z Sujet: Re: x+y+z=1/x+1/y+1/z  Mer 29 Aoû 2012, 15:12 Mer 29 Aoû 2012, 15:12 | |
| vous pouvez également montrer que : 4<=abc+a+b+c avec le même condition ... | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: x+y+z=1/x+1/y+1/z Sujet: Re: x+y+z=1/x+1/y+1/z  Mer 29 Aoû 2012, 15:59 Mer 29 Aoû 2012, 15:59 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: x+y+z=1/x+1/y+1/z Sujet: Re: x+y+z=1/x+1/y+1/z  Mer 29 Aoû 2012, 19:39 Mer 29 Aoû 2012, 19:39 | |
| - az360 a écrit:
- vous pouvez également montrer que : 4<=abc+a+b+c avec le même condition ...
C'est plutôt a+b+c +abc >= 2rac(3) ?? Voici: 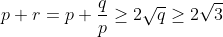 , on a: 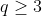 parce que: 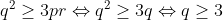 ... - younesmath2012 a écrit:
- bravo Mr "ali-mes" bonne et jolie reponse !!!
Merci.
Dernière édition par ali-mes le Dim 02 Sep 2012, 01:14, édité 1 fois | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 | |
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: x+y+z=1/x+1/y+1/z Sujet: Re: x+y+z=1/x+1/y+1/z  Mer 29 Aoû 2012, 21:24 Mer 29 Aoû 2012, 21:24 | |
| Oui, vous avez raison, excusez moi... | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: x+y+z=1/x+1/y+1/z Sujet: Re: x+y+z=1/x+1/y+1/z  Sam 01 Sep 2012, 15:58 Sam 01 Sep 2012, 15:58 | |
| proof of : a+b+c + abc >= 4
3*(a+b+c)/3 + abc >= 4sqrt[4](abc(a+b+c)^3 / (27)) = 4sqrt[4]((ab+bc+ca)(a+b+c)² / (27))
mais on a : ab+bc+ca >= 3 et (a+b+c)² >= 3(ab+bc+ca) >= 3 donc
(ab+bc+ca)(a+b+c)² >= 27 d'ou le resultat | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: x+y+z=1/x+1/y+1/z Sujet: Re: x+y+z=1/x+1/y+1/z  | |
| |
|
  | |
| | x+y+z=1/x+1/y+1/z |  |
|
