| | macedonia1999 |  |
|
|
| Auteur | Message |
|---|
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: macedonia1999 Sujet: macedonia1999  Lun 03 Sep 2012, 11:25 Lun 03 Sep 2012, 11:25 | |
| a,b,c>0 tq a²+b²+c²=3 MQ : 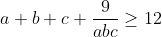 | |
|
  | |
Yassirhassininador
Habitué
 Nombre de messages : 12 Nombre de messages : 12
Age : 28
Localisation : Ensemble vide
Date d'inscription : 03/09/2012
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  Lun 03 Sep 2012, 14:32 Lun 03 Sep 2012, 14:32 | |
| a+b+c+9/(abc)>12. Est équivalent a a^2bc+...+(a^2+b^2+c^2)^2>12abc
On simplifie et d après AM-GM on trouve :
S>12abc | |
|
  | |
Yassirhassininador
Habitué
 Nombre de messages : 12 Nombre de messages : 12
Age : 28
Localisation : Ensemble vide
Date d'inscription : 03/09/2012
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  Lun 03 Sep 2012, 14:42 Lun 03 Sep 2012, 14:42 | |
| Alors comment vous avez trouve ma réponse ?  | |
|
  | |
killua 001
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 29
Localisation : Ma chambre :D
Date d'inscription : 02/05/2012
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  Lun 03 Sep 2012, 14:44 Lun 03 Sep 2012, 14:44 | |
| il suffit dde monttrer qu abc inf a 1 et a+b+c sup=3 et c fini | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  Lun 03 Sep 2012, 15:47 Lun 03 Sep 2012, 15:47 | |
| personne n'a trouvé la bonne reponse !!! | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  Lun 03 Sep 2012, 17:44 Lun 03 Sep 2012, 17:44 | |
| généralisation :
n >= 1 . tel que : a^n + b^n + c^n <= 3 montrer l'ineq.
+
je poste ma solution plus tard ... | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  Lun 03 Sep 2012, 19:48 Lun 03 Sep 2012, 19:48 | |
| on attend votre solution Mr ''az360'' !!! | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  Lun 03 Sep 2012, 19:57 Lun 03 Sep 2012, 19:57 | |
| voila : d'apres holder on a : (a+b+c) <= 3^(n-1)(a^n + b^n + c^n) <= 3^n
donc : p = a+b+c <= 3 et q = ab+bc+ca <= (a+b+c)²/3 <= 3
a+b+c + 9/abc >= a+b+c+81/(a+b+c)(ab+bc+ca) = p + 27/pq + 27/pq + 27/pq >= 4sqrt[4](3^9/(p²q^3)) >= 4*3 = 12
j'ai utilisé : pq >= 9abc . | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  Lun 03 Sep 2012, 20:04 Lun 03 Sep 2012, 20:04 | |
| - az360 a écrit:
- voila : d'apres holder on a : (a+b+c) <= 3^(n-1)(a^n + b^n + c^n) <= 3^n
donc : p = a+b+c <= 3 et q = ab+bc+ca <= (a+b+c)²/3 <= 3
a+b+c + 9/abc >= a+b+c+81/(a+b+c)(ab+bc+ca) = p + 27/pq + 27/pq + 27/pq >= 4sqrt[4](3^9/(p²q^3)) >= 4*3 = 12
j'ai utilisé : pq >= 9abc . la relation en rouge est fausse !!! vous pouver verifier pour n=4 on a a^4+b^4+c^4>=(a²+b²+c²)²/3 =3 on n'a pas le contraire!!!!! | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  Lun 03 Sep 2012, 20:05 Lun 03 Sep 2012, 20:05 | |
| nsiiit wahed ^n voila :
(a+b+c)^n <= 3^(n-1)(a^n + b^n + c^n) <= 3^n | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  Lun 03 Sep 2012, 20:08 Lun 03 Sep 2012, 20:08 | |
| - az360 a écrit:
- nsiiit wahed ^n voila :
(a+b+c)^n <= 3^(n-1)(a^n + b^n + c^n) <= 3^n la relation en rouge est fausse !!! vous pouver verifier pour n=4 on a a^4+b^4+c^4>=(a²+b²+c²)²/3 =3 on n'a pas le contraire!!!!! | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  Lun 03 Sep 2012, 20:14 Lun 03 Sep 2012, 20:14 | |
| moi j'ai montré ma generalisation ou il y'a : a^n + b^n + c^n <= 3 montrer l'ineq. donc ca reste vraiii ...
ou bien je nte comprend pas tjr !!
condition a²+b²+c² = 3 n'est pas encore valable ...
pour votre probleme il suffit de prend n = 2 et le cas d'egalité ... | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  Mar 04 Sep 2012, 09:12 Mar 04 Sep 2012, 09:12 | |
| 3=a²+b²+c²=p²-2q (notations habituelles)
3p=p^3-2pq >= 2pq-9r par schur
p+9/r >= 2pq/3-3r+9/r>= 3r+9/r car pq>=9r
p+9/r>= 4(3r.3/r.3/r.3/r)^(1/4)=12/r^(1/2)>=12 car 3=a²+b²+c²>=3r^(2/3) ==> r=<1 | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  Mar 04 Sep 2012, 10:06 Mar 04 Sep 2012, 10:06 | |
| bravo Mr "abdelbaki.attioui"
l'idee est la suivante : montrer que a+b+c >3abc | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  Mar 04 Sep 2012, 10:30 Mar 04 Sep 2012, 10:30 | |
| sans utiliser schur on peut repondre comme suit :
posons a+b+c=t et abc =r^3
on a 3=a²+b²+c² >=3r² donc r²<=1 ; a+b+c >=3r donc t/3r >=1
commençons d'abord: on a
[img]http://latex.codecogs.com/gif.latex?a+b+c+\frac{9}{abc}%20=t+\frac{3}{r^3}+\frac{3}{r^3}+\frac{3}{r^3}\geq%204\sqrt[4]{\frac{3^{3}t}{r^{9}}}=\frac{12}{r^{2}}\sqrt[4]{\frac{t}{3r}}\geq%2012\times%201=12[/img]
car 12/r² >=12 et t/3r >=1 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: macedonia1999 Sujet: Re: macedonia1999  | |
| |
|
  | |
| | macedonia1999 |  |
|
