| | Titu andreescu |  |
|
|
| Auteur | Message |
|---|
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Titu andreescu Sujet: Titu andreescu  Ven 07 Sep 2012, 21:12 Ven 07 Sep 2012, 21:12 | |
| | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Titu andreescu Sujet: Re: Titu andreescu  Sam 08 Sep 2012, 16:27 Sam 08 Sep 2012, 16:27 | |
| Pour le coté gauche: par absurde on prouve que l'un des réel a,b et c est unférieure ou égale à 1 ,par symétrie supposons que a=<1 ainsi : \geq&space;0\Leftrightarrow&space;ab+ac+bc-abc\geq&space;0) | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Titu andreescu Sujet: Re: Titu andreescu  Sam 08 Sep 2012, 16:42 Sam 08 Sep 2012, 16:42 | |
| | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Titu andreescu Sujet: Re: Titu andreescu  Dim 09 Sep 2012, 21:54 Dim 09 Sep 2012, 21:54 | |
| - younesmath2012 a écrit:
- et pour le coté droit ?
pour le coté droit: on peut facilement prouver qu'un des variable est inférieur ou égale à 1 et qu'un autre est supérieur ou égale à 1,supposons par symétrie que a=<1 et b>=1 si c>=1on a alors (c-1)(b-1)>=0 maintenant on a (4-c)}-bc}{2}) ça se trouve facilement , si on considère une équation d'inconnu a et donc (c-1)+bc+a\leq&space;a+bc=\frac{\sqrt{(4-b)(4-c)}-bc}{2}+bc=\frac{\sqrt{(4-b)(4-c)}+bc}{2}) et là il ne reste plus qu'applique C-S pour aboutir à : (4-c)}+bc}{2}\leq&space;2) le cas c=<1 se traite de la même façon en choisissant (a-1)(c-1). | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Titu andreescu Sujet: Re: Titu andreescu  Lun 10 Sep 2012, 03:46 Lun 10 Sep 2012, 03:46 | |
| - younesmath2012 a écrit:
-
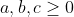 tq tq 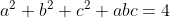 Mq: Mq: 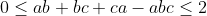 il me semble que c la 2eme fois que vous proposez ce problem Mr Younes , comme personne n'as tenté de résoudre l'inégalité de droite restante , je propose ma solution que j'avais garder en réserve ... Notons qu'il est claire que d'apres la condition est AM-GM , on a bien abc =< 1 . soit : (a-1)(b-1) >=0 =>ab+1 >= a+b => c +ab >= ab+bc+ca-abc , d'ou il suffit de prouver que : c+ab =< 2 . revenant a la condition on a : 4=a²+b²+c(c+ab) >= 2ab+c(c+ab) = (c+ab)(c+2)-2c => 4+2c >= (c+ab)(c+2) => c+ab =< (4+2c)\(c+2)=2 . Fin de la démonstration  . | |
|
  | |
Yassirhassininador
Habitué
 Nombre de messages : 12 Nombre de messages : 12
Age : 28
Localisation : Ensemble vide
Date d'inscription : 03/09/2012
 |  Sujet: Re: Titu andreescu Sujet: Re: Titu andreescu  Lun 10 Sep 2012, 11:08 Lun 10 Sep 2012, 11:08 | |
| En remplacent a=2x/ sqrt((x+y)(y+z)) ......en trouve la sol facilement | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Titu andreescu Sujet: Re: Titu andreescu  Lun 10 Sep 2012, 13:27 Lun 10 Sep 2012, 13:27 | |
| Bravo comme toujour Mr''oty'' | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Titu andreescu Sujet: Re: Titu andreescu  Mer 12 Sep 2012, 20:53 Mer 12 Sep 2012, 20:53 | |
| je pense que l' inégalité est aussi vrai (own) ;
soit a,b,c > 0 vérifiant : a²+b²+c²+abc=4 . Prouver que :
ab+bc+ca-abc =< 5\2 . | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Titu andreescu Sujet: Re: Titu andreescu  Mer 12 Sep 2012, 22:38 Mer 12 Sep 2012, 22:38 | |
| vous avez remplacer seulement 2 par 5/2 !!!
en effet on a ab+bc+ca-abc =<2 <5/2
| |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Titu andreescu Sujet: Re: Titu andreescu  Mer 12 Sep 2012, 23:13 Mer 12 Sep 2012, 23:13 | |
| - younesmath2012 a écrit:
- vous avez remplacer seulement 2 par 5/2 !!!
en effet on a ab+bc+ca-abc =<2 <5/2
oui mais je l'ai posté pour que quelqu'un essaye de la prouver directement , si on connaissait pas le probleme initial , il est pas trés naturel de constaté que LHS =< 2 . Mais oui 2 est une meilleur estimation . | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Titu andreescu Sujet: Re: Titu andreescu  | |
| |
|
  | |
| | Titu andreescu |  |
|
