f(x + y) = exp(x) f(y) + exp(y) f(x)

Trouver toutes les applications f : R --> R dérivables en 0 telles que :
qqs (x, y) dans R², f(x + y) = exp(x) f(y) + exp(y) f(x)

abdelbaki.attioui a écrit:: Trouver toutes les applications f : R --> R dérivables en 0 telles que :
qqs (x, y) dans R², f(x + y) = exp(x) f(y) + exp(y) f(x)

On a: $f(x + y) = exp(x) f(y) + exp(y) f(x) Gif.latex?(\forall (x,y)\in\mathbb{R}^2): f(x+y)=e^x.f(y)+e^y$ .
Si x=y=0, on aura $f(x + y) = exp(x) f(y) + exp(y) f(x) Gif$ , ce qui donnera $f(x + y) = exp(x) f(y) + exp(y) f(x) Gif$ .
D'autre part, on a $f(x + y) = exp(x) f(y) + exp(y) f(x) Gif.latex?(\forall (x,y)\in\mathbb{R}^2): f(x+y)-f(x)=e^x.f(y)+(e^y-1)$ .
Pour y non nul, on aura $f(x + y) = exp(x) f(y) + exp(y) f(x) Gif.latex?(\forall (x,y)\in\mathbb{R}\times\mathbb{R}^*): \frac{f(x+y)-f(x)}{y}=e^x.\frac{f(y)}{y}+\frac{e^y-1}{y}$ .
Cette égalité assure que si f est dérivable en 0, alors elle est dérivable partout.
En faisant tendre y vers 0, on aura $f(x + y) = exp(x) f(y) + exp(y) f(x) Gif.latex?(\forall x\in\mathbb{R}): f'(x)=e^x$ .==>(1)
Posons: $f(x + y) = exp(x) f(y) + exp(y) f(x) Gif.latex?(\forall x\in\mathbb{R}): g(x)=f(x)$ , on a $f(x + y) = exp(x) f(y) + exp(y) f(x) Gif.latex?(\forall x\in\mathbb{R}): g'(x)=f'(x).e^{-x}-f(x).e^{-x}=e^{-x}$ .
Selon 1, on aura: $f(x + y) = exp(x) f(y) + exp(y) f(x) Gif.latex?(\forall x\in\mathbb{R}): g'(x)=e^{-x}.e^x$ .
Donc g est de dérivée constante, elle est par suite de la forme: $f(x + y) = exp(x) f(y) + exp(y) f(x) Gif$ où a est une constante à déterminer.
Soit $f(x + y) = exp(x) f(y) + exp(y) f(x) Gif.latex?(\forall x\in\mathbb{R}): f(x)=f'(0).e^x.x+a$ où a est à déterminer lors de la prochaine étape.
Puisque $f(x + y) = exp(x) f(y) + exp(y) f(x) Gif$ , il vient que 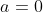$f(x + y) = exp(x) f(y) + exp(y) f(x) Gif$ .
Donc $f(x + y) = exp(x) f(y) + exp(y) f(x) Gif.latex?(\forall x\in\mathbb{R}): f(x)=f'(0).e^x$ .
Réciproquement, toute fonction de la forme $f(x + y) = exp(x) f(y) + exp(y) f(x) Gif.latex?f(x)=k.e^x$ répond au problème.
CQFD.
Sauf erreurs.

Maître Nombre de messages : 104 Date d'inscription : 16/01/2006

La continuité de f en 0 suffit pour conclure ! farao

sauf erreur bien entendu