| | Moscou 99 **** |  |
|
|
| Auteur | Message |
|---|
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Moscou 99 **** Sujet: Moscou 99 ****  Sam 09 Mar 2013, 17:38 Sam 09 Mar 2013, 17:38 | |
| bonsoir tout le monde
je vous propose un exo 4 etoils (hyper dur)
trouver tout les entiers n; k ;l et m tel que l>1 et
(1+n^k)^l =1+ n^m | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Sam 09 Mar 2013, 20:29 Sam 09 Mar 2013, 20:29 | |
| - n=0 est toujours solution!!! je crois qu'il faut étudier l'équation diophantienne si n différent de 0( et peut-être démontrer qu'il n'ya pas de solution)
Dernière édition par legend-crush le Sam 09 Mar 2013, 21:24, édité 1 fois | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Sam 09 Mar 2013, 20:57 Sam 09 Mar 2013, 20:57 | |
| | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Sam 09 Mar 2013, 21:23 Sam 09 Mar 2013, 21:23 | |
| ça doit être sur N pour m et k et l non??! | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Sam 09 Mar 2013, 21:36 Sam 09 Mar 2013, 21:36 | |
| au fait j'ai trouvé pls autres solutions!!! si m=l:  mais les trois dernière solutions marchent pas ^^!!
Dernière édition par legend-crush le Dim 10 Mar 2013, 10:06, édité 1 fois | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Dim 10 Mar 2013, 00:46 Dim 10 Mar 2013, 00:46 | |
| bon il est evident que si n=0 ca marche peut importe k,l,m si n=1 alors l=1 peut importe k et m mnt on a somme des (c(l,i)*n^(ki),i=1...l)=n^m avec m=qk+r on travaille dans Z/n^kZ l est divisible donc par n^k ca me donne somme des (c(l,i)*n^(ki-k),i=1...l)=n^(m-k) mais la puissance k dans la somme on la recupere en remplacant l par l=a1*n^k j'itere a1 est divisible par n^k a2... jusqu a aq en travaillant cette fois dans Z/n^rZ donc somme des (c(l,i)*n^(ki-m),i=1...l)=1 donc puisqu'on travaille dans N l=1 et m=k sauf erreur bien sur | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Dim 10 Mar 2013, 09:44 Dim 10 Mar 2013, 09:44 | |
| - galillee56 a écrit:
- bon il est evident que si n=0 ca marche peut importe k,l,m si n=1 alors l=1 peut importe k et m mnt on a somme des (c(l,i)*n^(ki),i=1...l)=n^m avec m=qk+r on travaille dans Z/n^kZ l est divisible donc par n^k ca me donne somme des (c(l,i)*n^(ki-k),i=1...l)=n^(m-k) mais la puissance k dans la somme on la recupere en remplacant l par l=a1*n^k j'itere a1 est divisible par n^k a2... jusqu a aq en travaillant cette fois dans Z/n^rZ donc somme des (c(l,i)*n^(ki-m),i=1...l)=1 donc puisqu'on travaille dans N l=1 et m=k sauf erreur bien sur
Au fait l=1 ne figure pas dans les solutions car l>1 Et s'il te plait pourrait-tu réecrir en utilisant le Latex http://www.codecogs.com/latex/eqneditor.php car j'ai rien compris dans ces ecritures!!! amicalement!! | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Dim 10 Mar 2013, 11:41 Dim 10 Mar 2013, 11:41 | |
| C'est que l'équation est équivalente à 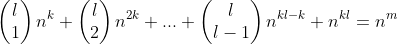 | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Dim 10 Mar 2013, 12:00 Dim 10 Mar 2013, 12:00 | |
| - Humber a écrit:
- On travaille dans Z ??
oui, cest dit "entiers", sans préciser, donc cest Z | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Dim 10 Mar 2013, 12:07 Dim 10 Mar 2013, 12:07 | |
| - elidrissi a écrit:
- Humber a écrit:
- On travaille dans Z ??
oui, cest dit "entiers", sans préciser, donc cest Z Tu es sûr que ce n'est pas entiers positifs ou positive integers en anglais ? | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Dim 10 Mar 2013, 13:05 Dim 10 Mar 2013, 13:05 | |
| complétant la maneuvre de Mr.Humber: en factorisant par n^k, on se rend compte que m est nécessairement un multiple de k. donc cette somme bonomiale, devrais s'écrire sous la forme de n^a ou a est un entier positif reportant dans la premiere equation, on obtient: (1+n^k)(1+n^k)^(l-1) =1+n^ak pour n=-1 ,a=2x+1 et k=2y+1 ou (x,y)£Z² toutes les valeurs en Z sont valables pour l pour n#-1 , ou n=-1 et (a#2x+1 ou k#2y+1 ) on pourras diviser les 2 cotés par 1+n^ak, dou (1+n^k)/(1+n^ak) = (1+n^k)^(1-l) et la je suis...bloqué  - Citation :
Tu es sûr que ce n'est pas entiers positifs ou positive integers en anglais ? oui c'est en français, et il ya juste "entiers", d'ou la dificultée du probleme | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Dim 10 Mar 2013, 19:49 Dim 10 Mar 2013, 19:49 | |
| - Humber a écrit:
- C'est que l'équation est équivalente à
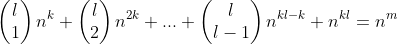 L doit pas être entier naturel pour utiliser cette equivalence??! | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Dim 10 Mar 2013, 20:25 Dim 10 Mar 2013, 20:25 | |
| - legend-crush a écrit:
- Humber a écrit:
- C'est que l'équation est équivalente à
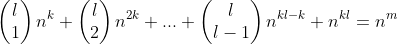
L doit pas être entier naturel pour utiliser cette equivalence??! Si mais je suis presque sûr que l'exercice est proposé pour l'ensemble N et pas Z . C'est pour cela .. | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Dim 10 Mar 2013, 20:55 Dim 10 Mar 2013, 20:55 | |
| bon come vous me croyez pas...  http://www.animath.fr/IMG/pdf/cours-arith1.pdf la page 74, exo 200 | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Dim 10 Mar 2013, 21:13 Dim 10 Mar 2013, 21:13 | |
| - elidrissi a écrit:
- bon come vous me croyez pas...

http://www.animath.fr/IMG/pdf/cours-arith1.pdf
la page 74, exo 200 - monsieur Elidrissi, tu n'aurais pas le lien de la deuxième partie, je la cherche depuis longtemps!!!! la solution est à la page 157( la dernière^^)!! Mais au fait dans leur solution, n=0 ne figure pas!! [u] | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Lun 11 Mar 2013, 13:38 Lun 11 Mar 2013, 13:38 | |
| @Legend-crush
non desolé, je le cherche de même
pour la solution, je l'ai vu tout a l'heure, et je pense qu'elle est incomplete, vu qu'il ya une infinité (litéralement) d'autres solutions | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Lun 11 Mar 2013, 17:57 Lun 11 Mar 2013, 17:57 | |
| En fait, je viens de trouver qu'il n'est pas encore Rédigé^^ | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Lun 11 Mar 2013, 19:25 Lun 11 Mar 2013, 19:25 | |
| jai entendu dire qu'il est sorti en anglais, je vais chercher. | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Mar 12 Mar 2013, 13:31 Mar 12 Mar 2013, 13:31 | |
| Dsl pour le retard c que mon pc plante du coup la j'utilise que mon telephone je ss vrmt dsl bref je vais poser les etapes les plus importantes et vous m aiderai aussi en me disant si il y a des fautes bon soit un nombre premier divisant n on va travailler dans z/p^mZ ca nous dis que phi(p^m)/l avec phi etant l'indicatrice d'euler ca c vrai pour n'importe quelle diviseur premier de n donc phi(n^m)/l donc l serai plus grand que n^(m-1) pas possible je m excuse si c ambigue je vais expliquer mon probleme j etais pas satisfait de ma premiere reponse un trop longue dc j ai cherche et j ai trouve celle ci mais ma preuve est valable si n ds z et les auts terme ds N ps:mr l idrissi je vois pas pk k/m en factorisant par n^k tu as juste k plus petit que m j attend vos remarque et dsl encore | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  Mar 12 Mar 2013, 16:08 Mar 12 Mar 2013, 16:08 | |
| @gallile oui oui ouiu dsl je me suis (tres largement ) emporté  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Moscou 99 **** Sujet: Re: Moscou 99 ****  | |
| |
|
  | |
| | Moscou 99 **** |  |
|
