La raison du niveau détérioré du Maroc en IMO

bonjour j'ai été parmis les participants du 2ème stage qui a pour buts de séléctionner la team du maroc en Imo 54 et j'ai proposé la solution suivante à un exo d'arithmétique proposé en stage mais ki a été étonnement refusé par l'un des correcteurs (on m'a donné 0/7 pour cette démonstration ) je vous demande juste de dire si vraiment cette démonstration mérite vraiment un 0/7
Bon l'exo est le suivant :

j'ai proposé cette solution :

Spoiler:

lamperouge a écrit:

bonjour j'ai été parmis les participants du 2ème stage qui a pour buts de séléctionner la team du maroc en Imo 54 et j'ai proposé la solution suivante à un exo d'arithmétique proposé en stage mais ki a été étonnement refusé par l'un des correcteurs (on m'a donné 0/7 pour cette démonstration ) je vous demande juste de dire si vraiment cette démonstration mérite vraiment un 0/7
Bon l'exo est le suivant :

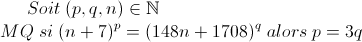
j'ai proposé cette solution :

Spoiler:

Bonsoir,


J'ai essayé de suivre ta démarche ligne par ligne, le flow me paraît correct (j'ai pas terminé , soudainement y a toute une montagne de cas qui surgit..) mais je trouve la note 0/7 pas juste ( un 1 ou 3 aurait pu être mieux allé keep calm and go )

L'équation de départ ==> n=2l+1
une substitution rapide nous conduit au résultat:

2^p.(l+4)^p=2^3q.(37l+232)^q (*)

le but est de prouver p=3q si on regarde bien l’équation (*) ( mais vraiment bien!! ) si on prouve l+4 est impaire (pareil pour l'autre ) c'est fini!
PGCD(l+4,37l+232) divise 84 et aussi divise 21l et donc divise 21.PGCD(l,4)
enfin une congruence module 4 pourrait aider:
==> On examine le cas l=0[4] et l=2[4] (le cas 1 et 3 résultat immédiat).
==> à suivre ..

l=2+4l' ==> p=2q ==> absurde
l=4l' ==> l+4=4(a+1)
si a =2b+1 (et enfin )
l'équation devient sauf erreur de ma part
2^(4p-6q)(b+1)^p=(37b+66)^q
et pgcd(b+1,37+66)|29 qui est premier
impair l'absurdité en découlera aprés [(prouvé par un pote)]

ouf trop de calcul, enfin je pense qu'il y a ptetre une méthode mieux que ça!!

lamperouge a écrit:

bonjour j'ai été parmis les participants du 2ème stage qui a pour buts de séléctionner la team du maroc en Imo 54 et j'ai proposé la solution suivante à un exo d'arithmétique proposé en stage mais ki a été étonnement refusé par l'un des correcteurs (on m'a donné 0/7 pour cette démonstration ) je vous demande juste de dire si vraiment cette démonstration mérite vraiment un 0/7
Bon l'exo est le suivant :

j'ai proposé cette solution :

Spoiler:

Tu as trouvé que (Car k=4).
Et la suite de la démonstration stipule que tu as pris: p=5 et q=4; ce qui n'est pas le cas.
En effet, ils existent deux entiers k et k' tels que p=5k et q=4k'; et puis k=k'.
Donc (p,q)=(5k,4k) avec k décrit l'ensemble des entiers naturels.
Autre chose, c'est que tu n'as pas le droit d'écrire car cette écriture n'est valide que si que tu n'a pas encore prouvé à ce stade.
Sauf errreur de compréhension de ma part!
Si tu m'apportes des explications en ce qui concerne ce que j'ai signalé, je peux continuer à lire ta solution...

nmo a écrit:

Tu as trouvé que (Car k=4).
Et la suite de la démonstration stipule que tu as pris: p=5 et q=4; ce qui n'est pas le cas.
En effet, ils existent deux entiers k et k' tels que p=5k et q=4k'; et puis k=k'.
Donc (p,q)=(5k,4k) avec k décrit l'ensemble des entiers naturels.
Autre chose, c'est que tu n'as pas le droit d'écrire car cette écriture n'est valide que si que tu n'a pas encore prouvé à ce stade.
Sauf errreur de compréhension de ma part!
Si tu m'apportes des explications en ce qui concerne ce que j'ai signalé, je peux continuer à lire ta solution...

En fait pour 4p=5q je n'ai po pris p=5 et q=4 mais plutot j'ai élevé l'équation à la puissance 4 puis remplacer 4p par 5q et utiliser l'identité de a^n-b^n=(a-b)(a^n-1+a^(n-2)b+...+b^n-1)
et pour ta remarque concernant k superieur strictement à 3 je l'ai dèja cité je ne vois tjrs po pk t'as dis que c'est invalide ^^

pour le cas de k inférieur à 3 c'estcomme si t'as multiplié puis divisé le m sur 2 ^^