- soukaina ella a écrit:
- une autre méthode pour résoudre cet exercice s'il vous plait
Exercice 89:
Soient f et g de fonction de [0;1] vers [0;1] tq f et g sont continues sur [0;1] .
on suppose que pour tout x€[0;1] fog(x)=gof(x)
Prouver qu'il existe a €[0;1] tq; f(a)=g(a)
Je propose une solution connue de ce problème:
Notons I=]
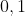
[.
Soit la fonction:
: h(x)=f(x)-g(x))
.
Puisque f et g sont deux fonctions continues, h l'est aussi.
On suppose que:
: h(x)\neq0)
.
Puisque h est continue, elle doit garder un signe constant.
On suppose par symétrie de f et g que:
: f(x)>g(x))
.
Et puisque f et g sont continues,
 : (\forall x\in I): f(x)\ge g(x)+a)
.
***On démontre que
:\underset{nfois}{\underbrace{fofo...of}}og=go\underset{nfois}{\underbrace{fofo...of}})
.
Le résultat se démontre par récurrence.
-L'initialisation est une donnée du problème.
-On suppose que pour un certain rang

, on a:
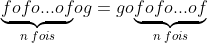
.
Et démontrons que:
fois}{\underbrace{fofo...of}}og=go\underset{(n+1)fois}{\underbrace{fofo...of}})
.
On a:
:\underset{n\;fois}{\underbrace{fofo...of}}og(x)=go\underset{n\;fois}{\underbrace{fofo...of}}(x))
.
Donc
:f(\underset{n\;fois}{\underbrace{fofo...of}}og(x))=f(go\underset{n\;fois}{\underbrace{fofo...of}}(x))=g(fo\underset{n\;fois}{\underbrace{fofo...of}}(x)))
.
Et par conséquent:
:\underset{(n+1)fois}{\underbrace{fofo...of}}og(x)=go\underset{(n+1)fois}{\underbrace{fofo...of}}(x))
.
-Conclusion de la récurrence:
 : \underset{n\;fois}{\underbrace{fofo...of}}og=go\underset{n\;fois}{\underbrace{fofo...of}})
.
De même, on démontre que:
 : \underset{n\;fois}{\underbrace{gogo...og}}of=fo\underset{n\;fois}{\underbrace{gogo...og}})
.
***On démontre que:
 : (\forall x\in I) :\underset{n\;fois}{\underbrace{fofo...of}}(x)\ge\underset{n\;fois}{\underbrace{gogo...og}}(x)+na)
.
-L'initialisation est triviale.
-On suppose que pour un certain entier n, on a
 :\underset{n\;fois}{\underbrace{fofo...of}}(x)\ge\underset{n\;fois}{\underbrace{gogo...og}}(x)+na)
.
Et démontrons que:
 :\underset{(n+1)fois}{\underbrace{fofo...of}}(x)\ge\underset{(n+1)fois}{\underbrace{gogo...og}}(x)+(n+1)a)
.
On a
 :\underset{(n+1)fois}{\underbrace{fofo...of}}(x)\ge\underset{n\;fois}{\underbrace{gogo...og}}(f(x))+na\ge fo\underset{n\;fois}{\underbrace{gogo...og}}(x)+na)
.
Or,
 fo\underset{n\;fois}{\underbrace{gogo...og}}(x)\ge go\underset{n\;fois}{\underbrace{gogo...og}}(x)+a=\underset{(n+1)fois}{\underbrace{gogo...og}}(x)+a)
.
Des deux inégalités précédantes, on déduit que:
 :\underset{(n+1)fois}{\underbrace{fofo...of}}(x)\ge\underset{(n+1)fois}{\underbrace{gogo...og}}(x)+a+an=\underset{(n+1)fois}{\underbrace{gogo...og}}(x)+(n+1)a)
.
-Conclusion de la récurrence:
 : (\forall x\in I) :\underset{n\;fois}{\underbrace{fofo...of}}(x)\ge\underset{n\;fois}{\underbrace{gogo...og}}(x)+na)
.
***Trouvons une absurdité, et concluons:
On a f est continue sur I, donc bornée et atteint ses bornes.
Il existe donc un réel M tel que
 :M\ge f(x))
.
Ainsi:
 : (\forall x\in I) :M\ge\underset{n\;fois}{\underbrace{fofo...of}}(x)\ge\underset{n\;fois}{\underbrace{gogo...og}}(x)+na)
.
En faisant tendre n vers

, absurde!
Ce qu'on a supposé est donc faux.
Ainsi,
: f(a)=g(a))
.
CQFD.
Sauf erreurs.
